ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ УПРАВЛЕНИЯ В ЗАДАЧАХ ОПТИМИЗАЦИИ ЭНЕРГОЗАТРАТ ТЯГОВОГО ПОДВИЖНОГО СОСТАВА
Aннотация
В работе средствами инволютивных распределений геометрической теории управления получена работоспособная линейная математическая модель движения дизель-поезда с двумя эквивалентными тяговыми электроприводами, которая эквивалентна нелинейной математической модели, описываемой системой нелинейных обыкновенных дифференциальных уравнений 24-го порядка с четырьмя управлениями. С помощью принципа максимума решены две задачи оптимального управления тяговым приводом: максимального быстродействия и минимизации взвешенной линейной комбинации времени и расходы квадрата управления. Это позволило, с одной стороны, получить для каждого участка железнодорожного пути законы управления, которые определяют минимально необходимое время для преодоления перегона, а с другой стороны, получать законы управления, обеспечивающие график движения и минимизацию расхода топливно-энергетических ресурсов.
Ключевые слова: геометрическая теория управления, линейная математическая модель, движение дизель-поезда, принцип максимума, оптимальное управление
Постановка проблемы и анализ литературы
Одним из основных стратегических направлений государственной политики Украины в области развития современных видов железнодорожного транспорта является привлечение к их производству отечественных производителей, что обеспечит уменьшения импортной зависимости Украинских железных дорог от зарубежных поставок подвижного состава [1, 2]. При этом особое внимание уделено, с одной стороны, внедрению современных энергосберегающих технологий, а с другой стороны, рациональному использованию имеющихся энергоресурсов [3]. Последнее решается путем совершенствования уже существующих систем автоматического управления подвижным составом с целью минимизации затрат энергоресурсов при соблюдении графиков движения. Для Украины этот вопрос является актуальным, поскольку расход энергоресурсов на перевозку грузов и пассажиров в нашей стране выше, чем в большинстве развитых стран мира.
Сегодня вопросами создания и совершенствования систем оптимального управления тяговым электроприводом подвижного состава занимается множество специалистов как в Украине, так и в странах ближнего и дальнего зарубежья. При этом работы этих ученых основываются на теории управления и теории оптимальных систем управления, а также методов динамического программирования, классического вариационного исчисления, принципа максимума Понтрягина, функций Ляпунова, аналитического конструирования Красовского и Летова-Калмана, терминального управления, синтеза робастных систем управления и т.д. [4 – 10]. Но, несмотря на это, в полном объеме проблема оптимального управления тяговым электроприводом подвижного состава не решена и по сей день, поскольку не решена проблема синтеза оптимальных систем управления для объектов c несколькими управлениями, которые описываются нелинейными системами обыкновенных дифференциальных уравнений высокого порядка. Это, в свою очередь, привело к разработке методов линеаризации исходных нелинейных систем и последующему применению хорошо разработанной теории линейных систем управления [11]. Однако наиболее часто применяемая линеаризация по Тейлору, позволяющая линеаризовать систему в достаточно малой окрестности выбранной рабочей точки, практически неприменима для сложных объектов, описываемых нелинейными системами обыкновенных дифференциальных уравнений высокого порядка. Но научная привлекательность теории управления линейными системами, которая позволяет синтезировать оптимальные системы управления для линейных объектов любого порядка, привела к разработке нового метода – геометрической линеаризации, основанного на геометрическом подходе к теории управления, теории групп, дифференциальной геометрии, алгебры Ли и т.д. Успехи этого метода линеаризации легли в основу создания нового научного течения – единой геометрической теории управления [12–14], которая с помощью обратной связи в пространстве «вход-выход» или «вход-состояние» позволяет преобразовывать нелинейные системы высокого порядка с несколькими управлениями в эквивалентные линейные системы. Это становится возможным благодаря декомпозиции исходной нелинейной модели объекта, представленной в некотором пространстве состояний, на ряд независимых линейных подсистем меньшей размерности в канонической форме Бруновского, которые принадлежат соответствующим подпространствам исходного пространства состояний. При этом каждая линейная подсистема уравнений содержит только одно управление [12].
Процесс получения линейного эквивалента для исходной нелинейной системы вида

, (1)
где  – вектор фазовых координат нелинейной системы управления на гладком многообразии М размерности n;
– вектор фазовых координат нелинейной системы управления на гладком многообразии М размерности n;  – гладкие векторные поля на многообразии М, которые в локальных системах координат имеют вид
– гладкие векторные поля на многообразии М, которые в локальных системах координат имеют вид  и
и  ;
;  ,
,  – гладкие функции векторного аргумента x, определенные в локальных системах координат на многообразии М;
– гладкие функции векторного аргумента x, определенные в локальных системах координат на многообразии М;  – управления, может быть сформулирован следующим образам: необходимо найти такую гладкую замену координат
– управления, может быть сформулирован следующим образам: необходимо найти такую гладкую замену координат  и управлений
и управлений  ,
,  (
(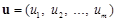 ), что система уравнений (1) приводится в новой системе координат к некоторой ей эквивалентной управляемой линейной системе
), что система уравнений (1) приводится в новой системе координат к некоторой ей эквивалентной управляемой линейной системе
 (2)
(2)
Здесь матрицы А и В имеют соответственно размеры n×n и n×m
и являются блочно-диагональными матрицами
 ,
,  , где
, где
 ;
;  ,
, 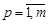 ,
,
где  ,
,  – индексы управляемости линейной системы управления (2),
– индексы управляемости линейной системы управления (2),  . При m=1, т.е. при скалярном управлении, система уравнений (2) сводится к канонической форме:
. При m=1, т.е. при скалярном управлении, система уравнений (2) сводится к канонической форме:

(3)
получившей название формы Бруновского. В случае векторного управления пространство  представляется в виде прямой суммы подпространств меньшей размерности:
представляется в виде прямой суммы подпространств меньшей размерности:  . При этом, каждое из подпространств
. При этом, каждое из подпространств  является подпространством состояний для р-й подсистемы декомпозированной исходной системы в пространстве
является подпространством состояний для р-й подсистемы декомпозированной исходной системы в пространстве  . Размерности подпространств, а следовательно, и размерности линейных подсистем в системе управления (2) однозначно определяются индексами управляемости
. Размерности подпространств, а следовательно, и размерности линейных подсистем в системе управления (2) однозначно определяются индексами управляемости  ,
,  линейной системы (2). Каждая линейная подсистема уравнений имеет одно управление и структуру системы уравнений вида (3), где число дифференциальных уравнений равно индексу управляемости. При этом решение, полученное при совместном интегрировании m независимых линейных подсистем уравнений, являющихся результатом декомпозиции исходной нелинейной системы уравнений в некоторой области
линейной системы (2). Каждая линейная подсистема уравнений имеет одно управление и структуру системы уравнений вида (3), где число дифференциальных уравнений равно индексу управляемости. При этом решение, полученное при совместном интегрировании m независимых линейных подсистем уравнений, являющихся результатом декомпозиции исходной нелинейной системы уравнений в некоторой области  пространства
пространства  не может в самом общем случае совпадать с решением нелинейной системы (1) в этой же области
не может в самом общем случае совпадать с решением нелинейной системы (1) в этой же области  . Для перехода от нелинейной системы уравнений (1) к канонической форме Бруновского необходимо, с одной стороны, определить индексы управляемости
. Для перехода от нелинейной системы уравнений (1) к канонической форме Бруновского необходимо, с одной стороны, определить индексы управляемости  (
( ), а с другой стороны, выполнения дополнительных условия – условия инволютивности распределений
), а с другой стороны, выполнения дополнительных условия – условия инволютивности распределений  [12], которые связанны с совместным интегрированием векторных полей на многообразии М.
[12], которые связанны с совместным интегрированием векторных полей на многообразии М.
В нашем случае с исходной нелинейной системой (1) связаны распределение 
векторных полей
 , где span – линейная оболочка
, где span – линейная оболочка  векторов в точке x (минимальное пространство, порожденное этим набором векторов) и распределение
векторов в точке x (минимальное пространство, порожденное этим набором векторов) и распределение  , где
, где 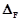 – распределение, смещенное на поле F относительно распределения
– распределение, смещенное на поле F относительно распределения  . С помощью указанных распределений
. С помощью указанных распределений  и
и 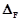 определяется следующие два семейства распределений:
определяется следующие два семейства распределений:

где [F, G] – скобки Ли двух векторных полей F, G, это векторное поле, характеризующее степень "связанности" на многообразии М полей F и G. В рассматриваемом случае они характеризуют возможность или ее отсутствие для совместного интегрирования задаваемых векторными полями F и G на гладком многообразии М уравнений в частных производных. Скобки Ли для векторных полей F, G в матричной форме, определяются следующим образом:
 ,
,
где
 ;
;
 ;
;  ;
; 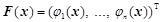 .
.
В случае неинволютивности распределений точная линеаризация возможна за счет увеличения размерности пространства и получения инволютивных распределений уже на расширенном пространстве [12].
Теоретически такой подход позволяет преобразовать к линейному виду широкий класс нелинейных систем управления, причем независимо от их размерности, однако его практическое применение, является чрезвычайно сложным и трудоемким, так как требует выполнения большого количества аналитических преобразований: вычисление производных и скобок Ли, а также дифференцирования функций вдоль соответствующих векторных полей на некотором многообразии и т.д., которые не автоматизированы ни в одном из известных пакетов моделирования. В связи с этим, в работах [15–17] были разработаны соответствующие функции для универсального пакета моделирования Matlab, позволяющие автоматизировать сложные аналитические преобразования геометрической линеаризации нелинейных математических моделей объектов, что, в свою очередь, устранило разрыв между теоретическими результатами геометрической теории управления и решением практических задач. Как следствие этого, появилась возможность применения геометрической теории управления для синтеза систем управления нелинейными объектами высокого порядка с несколькими управлениями. Однако определение оптимальных законов управления в каждой из подсистем не гарантирует оптимальность управления объектом в целом, поэтому необходим анализ полученных результатов оптимизации и, при необходимости, корректировка полученных результатов.
Цель работы. Оптимизация законов управления движением дизель-поезда с тяговым электроприводом на основе динамической линеаризации математической модели объекта управления средствами инволютивных распределений геометрической теории управления.
Математическая модель движения дизель-поезда состоящего из трех вагонов [15], учитывающая, с одной стороны, основные виды колебаний вагонов подвижного состава и распределение сил взаимодействия между ними, а с другой стороны, параллельную работу эквивалентных тяговых асинхронных двигателей двух обмоторенных вагонов, может быть представлена следующей системой нелинейных дифференциальных уравнений с четырьмя управлениями:

где y1 – расстояние, проходимое дизель-поездом и отсчитываемое от начала перегона; t – время; 
– постоянные коэффициенты, которые учитывают параметры двух эквивалентных приводов обмоторенных вагонов и подвижного состава;
 – скорости движения, соответственно первого, второго и третьего вагонов дизель-поезда;
– скорости движения, соответственно первого, второго и третьего вагонов дизель-поезда; 
– силы, действующие между соответственно первым и вторым, и вторым и третьим вагонами поезда;

и
 – проекции на оси α и β потокосцеплений статоров эквивалентных двигателей соответственно первого и второго обмоторенных вагонов;
– проекции на оси α и β потокосцеплений статоров эквивалентных двигателей соответственно первого и второго обмоторенных вагонов;  и
и  – проекции на оси α и β напряжений обмоток статоров эквивалентных двигателей соответственно первого и второго обмоторенных вагонов;
– проекции на оси α и β напряжений обмоток статоров эквивалентных двигателей соответственно первого и второго обмоторенных вагонов;  и
и  – проекции на оси α и β потокосцеплений роторов эквивалентных двигателей соответственно первого и второго обмоторенных вагонов; y9 и y21 – угловые скорости вращения роторов двигателей соответственно первого и второго обмоторенных вагонов;
– проекции на оси α и β потокосцеплений роторов эквивалентных двигателей соответственно первого и второго обмоторенных вагонов; y9 и y21 – угловые скорости вращения роторов двигателей соответственно первого и второго обмоторенных вагонов; y7 – величина бокового отклонения второго вагона;
 – промежуточные переменные; y19
– промежуточные переменные; y19 – угол виляния второго вагона.
С помощью инволютивных распределений геометрической теории управления в пространстве «вход – состояние» исходная нелинейная математическая модель движения дизель-поезда может быть преобразована к следующей линейной системе в канонической форме Бруновского:

(4)
где  (
( ) – управления.
) – управления.
Для данной математической модели определяются функции  (
( ), преобразующие переменные исходной нелинейной модели объекта управления в переменные линейной модели в форме Бруновского:
), преобразующие переменные исходной нелинейной модели объекта управления в переменные линейной модели в форме Бруновского: 


 Методика определения этих функций описана в работах [12, 15–17]. Из этих функций путем последовательного дифференцирования можно получить выражения для определения переменных:
Методика определения этих функций описана в работах [12, 15–17]. Из этих функций путем последовательного дифференцирования можно получить выражения для определения переменных:  из функции
из функции 
;
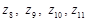 из функции
из функции  ;
;  из функции
из функции 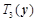
;
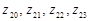 из функции
из функции  . Благодаря этому были получены функции, связывающие переменные в линейной и нелинейной моделях.
. Благодаря этому были получены функции, связывающие переменные в линейной и нелинейной моделях.
Для первой подсистемы уравнений в форме Бруновского получено





Для второй подсистемы уравнений в форме Бруновского получено

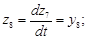



Аналогично получены функции, связывающие переменные в линейной и нелинейной моделях для третей и четвертой подсистемы уравнений в канонической форме Бруновского получено:
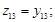



…………………………………………………




…………………………………………………
Таким образом, исходная нелинейная математическая модель движения дизель-поезда 24-го порядка была разбита на четыре независимых линейных подсистем шестого порядка в канонической форме Бруновского, каждая из которых содержит только одно управление.
Линейная математическая модель объекта управления в форме Бруновского состоит из четырех одинаковых по внешнему виду подсистем дифференциальных уравнений, которые описывают эквивалентные асинхронные электроприводы двух обмоторенных вагонов дизель-поезда. Поскольку электроприводы в обмоторенных вагонах в первом приближении можно рассматривать как одинаковые, то будем определять оптимальные управления только для одного эквивалентного асинхронного привода, управление которым осуществляется путем изменения амплитуды и частоты питающего напряжения. Так как при управлении тяговым приводом часто выдерживают определенные соотношения между амплитудой и частотой питающего напряжения (например, отношение амплитуды к частоте равно константе), то можно осуществлять поиск только одного из управлений, например, амплитуды питающего напряжения.
В зависимости от требований, предъявляемых к движению состава, можно сформулировать две основных задачи оптимального управления тяговым приводом: максимального быстродействия и минимизации взвешенной линейной комбинации времени и расхода квадрата управления.
Решим вначале с помощью принципа максимума Понтрягина задачу максимального быстродействия. Поскольку линейная модель объекта управления в форме Бруновского (4) состоит из четырех одинаковых по внешнему виду подсистем дифференциальных уравнений, то можно рассматривать определение управления  , минимизирующего функционал
, минимизирующего функционал

(5)
где  и
и  – начало и конец интервала управления, только для одной из подсистем – первой:
– начало и конец интервала управления, только для одной из подсистем – первой:
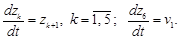
(6)
Необходимо найти управление  , минимизирующее функционал (5) при переводе объекта (6) из начального состояния
, минимизирующее функционал (5) при переводе объекта (6) из начального состояния  в конечное состояние
в конечное состояние  ,
, . При этом на управление
. При этом на управление  наложены ограничения:
наложены ограничения:
 ;
;  ,
,  . (7)
. (7)
Запишем функцию Гамильтона:

(8)

где  – дополнительная фазовая переменная, учитывающая наличие функционала (5);
– дополнительная фазовая переменная, учитывающая наличие функционала (5);  – сопряженные переменные; G – область допустимых управлений, задаваемая неравенствами (7).
– сопряженные переменные; G – область допустимых управлений, задаваемая неравенствами (7).
В силу линейности гамильтониана (8) по отношению к управлению получаем, что он достигает своего максимального значения при условии, что управление
 по своему знаку противоположно сопряженной переменной
по своему знаку противоположно сопряженной переменной  :
:

(9)
Сопряженные переменные  определяются из системы дифференциальных уравнений
определяются из системы дифференциальных уравнений

(10)
где  – значения сопряженных переменных в конечный момент интервала управления.
– значения сопряженных переменных в конечный момент интервала управления.
Выполняя дифференцирование правых частей уравнений (10), с учетом выражения (8), получим:

(11)
Интегрируя дифференциальные уравнения (11), найдем сопряженные переменные:

(12)
где  – константы.
– константы.
Так как константы  неизвестны, то применение принципа максимума Понтрягина приводит на этом этапе к качественному описанию изменения управления. Поскольку функция
неизвестны, то применение принципа максимума Понтрягина приводит на этом этапе к качественному описанию изменения управления. Поскольку функция  может менять знак не более пяти раз, то и управление
может менять знак не более пяти раз, то и управление может иметь не более пяти изменений знака управления, т.е. не более шести интервалов постоянства управления. Однако в рассматриваемом случае решение существенно упрощается, поскольку при ровном участке железнодорожного пути перевозка пассажиров дизель-поездом начинается с разгона, достижения максимальной скорости, движения с этой скоростью, а затем – торможение и остановка, то есть наблюдается только два интервала постоянства управления. Время переключения с одного постоянного управления на другое может быть определено с помощью итерационной процедуры. Переменный профиль пути на равнинной местности не вносит существенных изменений в закон управления, однако время переключения с одного управления на другое может изменяться и может не быть интервала времени с постоянной скоростью движения.
При решении задачи минимизации взвешенной линейной комбинации времени движения и расхода квадрата управления, объект управления описывается системой уравнений (6), а управление определяется из условия минимума функционала:

(13)
где  – постоянный коэффициент.
– постоянный коэффициент.
Основные соотношения принципа максимума Понтрягина имеют вид:

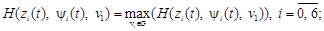

 , (14)
, (14)
где G – область допустимых управлений, задаваемая неравенствами (7);  ,
,  – значения фазовых переменных соответственно в начальный и конечный момент времени
– значения фазовых переменных соответственно в начальный и конечный момент времени 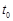 ,
,  ,
,  ;
; 
– значения сопряженных переменных в конечный момент времени
 ,
,  .
.
Сопряженные переменные  , как и в задаче максимального быстродействия, определяются соотношениями (11).
, как и в задаче максимального быстродействия, определяются соотношениями (11).
Если управление  в режиме тяги находится внутри допустимой области управлений G, тогда справедливы соотношения
в режиме тяги находится внутри допустимой области управлений G, тогда справедливы соотношения

По основной теореме принципа максимума [18] вектор сопряженных переменных  определен с точностью до произвольного постоянного положительного множителя и
определен с точностью до произвольного постоянного положительного множителя и  (ситуация анормальных вариационных задач, когда
(ситуация анормальных вариационных задач, когда  , не рассматривается, поскольку решаемая задача к этому классу не относится), поэтому можно принять:
, не рассматривается, поскольку решаемая задача к этому классу не относится), поэтому можно принять: 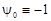 .
.
В рассматриваемой задаче в интервале времени управления режимом тяги выполняется равенство
 . (15)
. (15)
Имея два интеграла Н и  уравнений движения, можно с помощью скобок Пуассона получить третий интеграл движения [19]:
уравнений движения, можно с помощью скобок Пуассона получить третий интеграл движения [19]:

(16)
или
 , (17)
, (17)
где  – скобки Пуассона интегралов Н и
– скобки Пуассона интегралов Н и  уравнений движения.
уравнений движения.
Из выражений (12) и (17) следует, что  , поэтому
, поэтому и
 .
.
Таким образом, при  ,
,  имеем:
имеем:
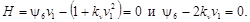
(18)
Исключая  из выражений (18), получим
из выражений (18), получим 
При малых значениях  управление
управление  в режиме тяги может превосходить
в режиме тяги может превосходить 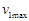 , т.е. выходить за пределы допустимой области управлений, поэтому оно должно определяться соотношением:
, т.е. выходить за пределы допустимой области управлений, поэтому оно должно определяться соотношением:

Определим минимально допустимое значение коэффициента
 , которое имеет смысл использовать в функционале (13):
, которое имеет смысл использовать в функционале (13):

Следовательно, только при
решение рассматриваемой задачи будет отличаться от решения задачи максимального быстродействия.
Исходя из изложенного можно сделать вывод о том, что для уменьшения расхода энергии или топлива, необходимого на перемещение состава с различной загрузкой из начального в конечный пункт назначения за определенное время, машинисту необходимо вести дизель-поезд с минимально возможной скоростью, при которой обеспечивается заданный расписанием график движения по перегону.
Однако знание оптимальных управлений для каждой головки дизель-поезда не гарантирует оптимального управления всем составом, что подтверждается и практикой эксплуатации. Как показывает практика движения дизель-поездов ДЭЛ-02 на маршрутах пригородного сообщения Одесской железной дороги при перевозке пассажиров на равнинной местности (когда переменный профиль пути не вносит существенных изменений в закон управления), расход энергоресурсов при ведении подвижного состава с помощью двух головок дизель-поезда, работающих синхронно на одинаковых позициях контроллера машиниста, выше, чем при ведении состава на одной головке поезда с полностью выключенной второй головкой (в летний период года), или с частично включенной второй головкой (в зимний период), когда необходима выработка энергии для внутренних нужд поезда и обогрева вагонов. При этом меньший расход энергоресурсов наблюдается даже несмотря на то, что машинисту приходится осуществлять более интенсивный разгон состава на одной головке с помощью более высоких тяговых позиций контроллера машиниста до большей скорости движения, а также осуществлять интенсивное торможение для выдерживания времени, связанного с расписанием движения поезда по данному маршруту.
Рассмотрим примеры движения дизель-поезда между двумя станциями маршрута на равном участке железнодорожного пути длинной L = 3 км за время t = 5 мин с учетом действующих ограничений на скорость (V ≤ 50 км/ч) и максимальное значение ускорения a при ведении подвижного состава связанных с комфортом поездки пассажиров в режимах разгона и торможения 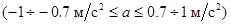 . На рис. 1 представлены графики изменения во времени позиций тягового (NКМ) и тормозного (NТКМ) контроллеров машиниста, скорости движения первого, второго и третьего вагонов дизель-поезда (
. На рис. 1 представлены графики изменения во времени позиций тягового (NКМ) и тормозного (NТКМ) контроллеров машиниста, скорости движения первого, второго и третьего вагонов дизель-поезда ( ), ускорения первого вагона поезда (a), пройденного пути (
), ускорения первого вагона поезда (a), пройденного пути ( ), силы, действующие между первым и вторым (
), силы, действующие между первым и вторым ( ), и вторым и третьим вагонами поезда (
), и вторым и третьим вагонами поезда ( ), а также расходов энергии (Е) потребленной дизель-поездом при движении между двумя станциями. При этом на рис. 1, а, в представлены графики процессов при одновременном использовании в процессе движения двух моторных вагонов дизель-поезда, работающих синхронно на 1 – 3 позициях тягового контроллера машиниста в режиме разгона поезда (с 0 по 80 сек) и на 2 позиции в режиме поддержания заданной максимальной скорости (V = 50 км/ч) движения (с 81 по 245 сек), а на рис. 1, б, г – при использовании одного моторного вагона дизель-поезда работающей на 1–6 позициях тягового контроллера машиниста в режиме разгона поезда (с 0 по 145 сек) и на 4 позиции в режиме поддержания заданной максимальной скорости (V = 50 км/ч) движения (с 146 по 245 сек).
), а также расходов энергии (Е) потребленной дизель-поездом при движении между двумя станциями. При этом на рис. 1, а, в представлены графики процессов при одновременном использовании в процессе движения двух моторных вагонов дизель-поезда, работающих синхронно на 1 – 3 позициях тягового контроллера машиниста в режиме разгона поезда (с 0 по 80 сек) и на 2 позиции в режиме поддержания заданной максимальной скорости (V = 50 км/ч) движения (с 81 по 245 сек), а на рис. 1, б, г – при использовании одного моторного вагона дизель-поезда работающей на 1–6 позициях тягового контроллера машиниста в режиме разгона поезда (с 0 по 145 сек) и на 4 позиции в режиме поддержания заданной максимальной скорости (V = 50 км/ч) движения (с 146 по 245 сек).
Как видно из графиков на рис. 1 расход энергии E при ведении подвижного состава с помощью двух обмоторенных вагонов дизель-поезда, работающих синхронно на одинаковых позициях контроллера машиниста выше, чем при ведении состава с помощью одного обмоторенного вагона поезда с полностью выключенным вторым обмоторенным вагоном. Это связано с тем, что на нижних позициях контроллера машиниста к.п.д. использования топлива для реализации управления меньше чем на высших позициях контроллера машиниста. Так, например, суммарная мощность, которая вырабатывается двумя тяговыми генераторами дизель-поезда ДЭЛ-02 для реализации второй позиции контроллера машиниста при поддержании скорости движения поезда V1 = 50 км/ч (рис. 1, а, с 81 по 245 сек), при условии синхронного использования двух обмоторенных вагонов, выше, чем мощность, которую вырабатывает тяговый генератор первого обмоторенного вагона дизель-поезда для реализации четвертой позиции контроллера машиниста (рис. 1, б, с 146 по 245 сек) при поддержании той же скорости движения подвижного состава (табл. 1).

Рис. 1. Графики полученные при движении дизель-поезда на равном участке пути с использованием:
а, в – двух тяговых головок (синхронно); б, г – одной тяговой головки
Fig. 1. Graphs of a diesel train moving on the level track with the use of: а, в – 2 traction drives (in synchronism); б, г – one traction drive
Таблица 1
Частота вращения (nд) и тягового генератора (Pг) по позициям контроллера машиниста (КМ)
Table 1
Rotation rate (nд) and traction generator (Pг) by reference to the main controller (KM)
Позиция КМ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
nд, мин-1 | 800 | 800 | 1000 | 1200 | 1400 | 1600 | 1800 | 2000 | 2100 |
Pг, кВт | 83 | 83 | 128 | 190 | 246 | 333 | 386 | 432 | 472 |
Следовательно, необходима модификация метода оптимизации энергозатрат тягового подвижного состава, связанная с введением дополнительного этапа поиска оптимальных управлений, т.е. оптимизацию необходимо проводить в несколько этапов, один из которых предполагает поиск оптимальных управлений на уровне тяговых электроприводов обмоторенных вагонов дизель-поезда, а другой, оптимизацию на уровне движения всего состава по железнодорожным перегонам.
Заключение
Средствами инволютивных распределений геометрической теории управления получена работоспособная линейная математическая модель движения дизель-поезда с двумя эквивалентными тяговыми электроприводами, которая эквивалентна нелинейной математической модели, описываемой системой нелинейных обыкновенных дифференциальных уравнений 24-го порядка с четырьмя управлениями. Число уравнений в этой модели, по меньшей мере, в пять раза больше, чем в известных примерах, где применяется геометрическая теория управления. С помощью полученной модели и принципа максимума Понтрягина решены две задачи оптимального управления дизель-поездом.
















Список литературы