ОПИСАНИЕ КЛАССА ВХОДНЫХ СИГНАЛОВ СИСТЕМЫ УПРАВЛЕНИЯ
Aннотация
В статье рассматривается метод определения класса входных сигналов линейной системы управления с непрерывным временем. Класс входных сигналов линейной системы управления с непрерывным временем описывается обыкновенным дифференциальным уравнением. Получена оценка установившейся ошибки управления. Приводится пример решения задачи.Ключевые слова: системы управления, входные сигналы, дифференциальное уравнение, установившаяся ошибка
К сожалению, текст статьи доступен только на Английском
Introduction
The quality of the synthesized control system depends on utilization of information about input signals. Therefore, the so-called absorption principle [7] in the automatic control theory is widespread. The absorption principle is built on class description of the input signals by homogeneous differential or difference equations with arbitrary initial conditions [1, 3–5, 8–11]. In this paper, the larger class of input signals of a continuous-time linear control system is specified by the stationary heterogeneous differential equation with arbitrary initial conditions and a restricted right member [2, 6]. This approach can be easily extended to discrete systems.
1. Statement of the problem
Let
 ,
,  , (1)
, (1)
be transfer functions corresponding to a desirable control system and a synthesized control system, where 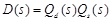 is a stable polynomial.
is a stable polynomial.
In this paper, we shall determine the signals class  such that
such that
 (2)
(2)
here
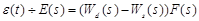 ,
, 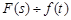 . (3)
. (3)
2. Main results
Consider the error E(s) determined by (3). Using (1), we get
 (4)
(4)
or
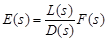 , (5)
, (5)
where 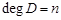 ,
, 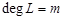 , and
, and
 . (6)
. (6)
We show that the input signals class  is defined by the set of solutions of the linear differential equation
is defined by the set of solutions of the linear differential equation
 ,
,  , (7)
, (7)
with arbitrary initial conditions and a piecewise continuous restricted right member, i.e.,
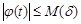
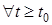 ,
,  . (8)
. (8)
Here  and
and  is piecewise continuous. Next we define
is piecewise continuous. Next we define  . The application of the Laplace transformation to equation (7) yields
. The application of the Laplace transformation to equation (7) yields
 , (9)
, (9)
where L0 is a polynomial of degree m-1. Note that the Laplace transformation of the functions  ,
, 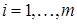 and
and 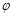 is existed. Combining (5) and (9), we obtain
is existed. Combining (5) and (9), we obtain
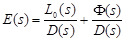 . (10)
. (10)
Since D(s) is the Hurwitz polynomial, it follows that
 . (11)
. (11)
Here
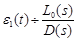 (12)
(12)
is a transient components of the error ε(t). We can therefore write
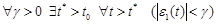 . (13)
. (13)
Let us consider now a steady-state components
 (14)
(14)
— of the error ε(t). Let
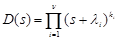 ,
,  ,
, 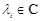 ,
, 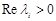 . (15)
. (15)
Then
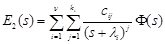 , (16)
, (16)
where
 . (17)
. (17)
By the convolution theorem, we have
 . (18)
. (18)
Taking into account (8), we get
 . (19)
. (19)
It can easily be checked that
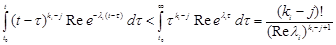 . (20)
. (20)
Finally, we obviously obtain the estimate
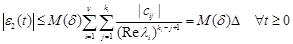 , (21)
, (21)
where cij is given by (17) and
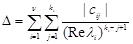 . (22)
. (22)
Combining (21) and (13), we get the following proposition:
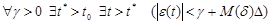 . (23)
. (23)
Let  and
and
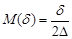 . (24)
. (24)
Thus proposition (2) is executed for the input signals satisfying conditions (7), (8), and (24).
Notice that relationships (17) and (22) indicate the practical methods for the decrease of the steasy-state error. If 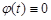 , then the steady-state error is equal to 0.
, then the steady-state error is equal to 0.
3. Example
Let us consider
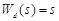 ,
, 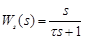 ,
, 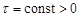 . (25)
. (25)
Therefore,
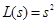 ,
,  . (26)
. (26)
From (22), we obtain  . Thus the signals class
. Thus the signals class  is defined by the following conditions:
is defined by the following conditions:
 , (27)
, (27)
 . (28)
. (28)
This implies that
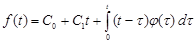 ,
,  . (29)
. (29)
Clearly, algebraic polynomials of degree 1, trigonometric polynomials, decreasing exponents, and logarithmic functions belong to the selected class  . Note also that the class
. Note also that the class 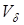 are not exhausted the listed functions.
are not exhausted the listed functions.
Let us consider now
 ,
, 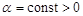 . (30)
. (30)
Hence,
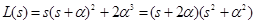 ,
, 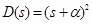 . (31)
. (31)
Using (22), we get  . Consequently the signals class
. Consequently the signals class  is determined by the equation
is determined by the equation
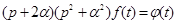 ,
,  , (32)
, (32)
where
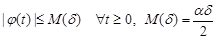 . (33)
. (33)
If 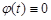 , then the element with transfer function (30) realizes the asymptotically fine noise-proof differentiating of amplitude modulated signals
, then the element with transfer function (30) realizes the asymptotically fine noise-proof differentiating of amplitude modulated signals

 . (34)
. (34)
















Список литературы
Список использованной литературы появится позже.