ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭКСПЕРТНОЙ СИСТЕМЫ С ПРАВИЛОМ ВЫВОДА НА ОСНОВЕ НЕЧЁТКОЙ СТЕПЕНИ ИСТИННОСТИ
Aннотация
Рассмотрен процесс нечёткого вывода, основанного на нечёткой степени истинности для построения нечётких систем вывода. Системы нечёткого логического вывода играют важную роль в многочисленных приложениях теории нечётких множеств, таких как нечёткие экспертные системы и многое другие. В основе таких систем лежат логические правила вида «Если …, то …», в которых посылки и выводы являются нечёткими понятиями. Использование нечётких множеств и нечёткой степени истинности вместе с композиционным правилом вывода Заде позволяет построить такую экспертную систему, которая может оперировать как с нечёткими, так и с чёткими входными данными. С другой стороны, использование нечёткой степени истинности значительно повышает эффективность решения задач, так как уменьшается вычислительная сложность алгоритма.
Ключевые слова: процесс нечёткого вывода, нечёткая степень истинности, нечёткие множества, нечёткие системы вывода, композиционное правило вывода Заде
Введение
Нечёткие системы широко используются вот многих областях техники в течение нескольких десятилетий [8]. Их популярность основана на простом и понятном подходе к неопределённости, которая неизбежна при рассмотрении и оценке процессов окружающего мира. На протяжении многих лет исследователи разработали различные подходы к проблеме нечёткого вывода. Теоретические основы были введены Заде [9] и с тех пор были предложены другие решения. Самыми популярными в приложениях являются подходы, представленные Мамдани [4], Ларсен [5], Токаги [15], Сугенто [15], а также Цукамато [7].
Эти решения, как правило, используются из-за простоты и эффективности их реализации. Вместе с тем методы не в полной мере соответствуют теории Заде из-за значительного упрощения. Причина может быть замечена для систем со многими нечёткими входами т.е. когда функции принадлежности фактов отличаются от синглтонов.
Как известно, частным случаем композиционного правила вывода является обобщённое правило modus ponens, которое описывается соотношением [9].
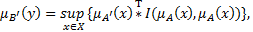
где 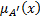 ,
, 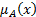 ,
, 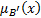 ,
, 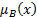 – функция принадлежности,
– функция принадлежности,  – t-норма представляющая, пересечение нечёткого факта
– t-норма представляющая, пересечение нечёткого факта 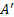 и нечёткой импликации I, аргументом которой является посылка A и вывод B. Нечёткие множества описываются на пространстве рассуждений X и факта, и на Y для заключения B и результата вывода B. К сожалению, для составных посылок вычисление по вышеприведённому методу становится очень сложным из-за многомерного анализа. Это является основной причиной, по которой метод в указанном виде не используется для очень распространённых правил с составной посылкой, содержащей многочисленные связи. Например, решений на основе интеллектуального анализа данных для классификации генов, производящих правила с тысячами посылок [3].
и нечёткой импликации I, аргументом которой является посылка A и вывод B. Нечёткие множества описываются на пространстве рассуждений X и факта, и на Y для заключения B и результата вывода B. К сожалению, для составных посылок вычисление по вышеприведённому методу становится очень сложным из-за многомерного анализа. Это является основной причиной, по которой метод в указанном виде не используется для очень распространённых правил с составной посылкой, содержащей многочисленные связи. Например, решений на основе интеллектуального анализа данных для классификации генов, производящих правила с тысячами посылок [3].
Важным преимуществом подхода, предлагаемого в статье является вывод в рамках единого пространства истинности для всех посылок. Это достигается за счёт преобразования отношений между фактом и посылкой в так называемую нечёткую степень истинности. Приведение всех отношений между различными фактами и посылками в одно нечёткое пространство истинности упрощает вычисление составной функции истинности. Поэтому данный подход лишён проблем многомерного анализа и лучше подходит для решения задач интеллектуального анализа.
Данный подход имеет, обладает экспоненциально возрастающей сложностью вычисления выхода при увеличении количества входов в системе, или если входные величины представляют из себя нечёткие значения. Можно упростить процесс вывода, используя понятие нечёткой степени истинности.
1. Постановка задачи
Задача, которая решается с помощью нечёткой продукционной системы формируется следующим образом. Рассмотрим систему с n входами 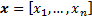 и одним входом y. Взаимосвязь входов и выхода описывается с помощью N нечётких правил представленных в виде:
и одним входом y. Взаимосвязь входов и выхода описывается с помощью N нечётких правил представленных в виде:
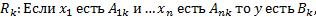
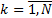 (1.1)
(1.1)
где 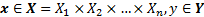 и
и 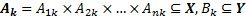 являются нечёткие множества.
являются нечёткие множества.
Особенность систем логического типа согласно классификации, произведённой в [1] состоит в том, что правило (1) формализуется с использованием нечёткой импликации в виде нечёткого (n+1)-арного отношения 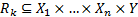 следующим образом:
следующим образом:
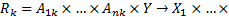
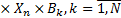
где «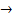 » – нечёткая импликация, выражающая причинно-следственную связь между антецедентом «
» – нечёткая импликация, выражающая причинно-следственную связь между антецедентом «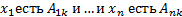 » и консеквентом «
» и консеквентом «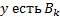 ». Ставится задача – определить нечёткий вывод
». Ставится задача – определить нечёткий вывод 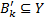 для системы представленной в виде (1), если на входах – нечёткие множества
для системы представленной в виде (1), если на входах – нечёткие множества 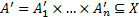 или
или 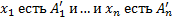 .
.
2. Методвывода на основе нечёткой степени истинности
Нечёткий выход 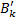 для систем с n входами с использованием нечёткой степени истинности (НСИ) основанный на обобщённом правиле modus ponens [9], следуя [13] записывается следующим образом:
для систем с n входами с использованием нечёткой степени истинности (НСИ) основанный на обобщённом правиле modus ponens [9], следуя [13] записывается следующим образом:
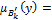
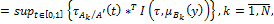 (2.1)
(2.1)
где 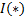 – операция нечёткой импликации;
– операция нечёткой импликации;  – t-норма;
– t-норма; 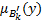 и
и 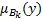 – функции принадлежности нечётких множеств
– функции принадлежности нечётких множеств 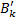 ,
, 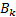 соответственно.
соответственно. 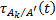 – функция принадлежности НСИ
– функция принадлежности НСИ 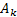 при условии, что
при условии, что 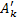 истинно, которая при независимых входах в соответствии с [13] равняется:
истинно, которая при независимых входах в соответствии с [13] равняется:
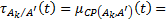
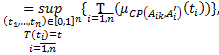 (2.2)
(2.2)
где 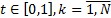 ;
; 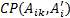 – нечёткая степень совместимости
– нечёткая степень совместимости 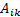 со входным нечётким значением
со входным нечётким значением 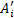 . Используя обозначение степени совместимости, (2.2) может быть записана следующим образом:
. Используя обозначение степени совместимости, (2.2) может быть записана следующим образом:
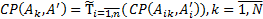 (2.3)
(2.3)
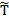 – расширенная по принципу обобщения n-местная t-норма [1]. Используя наиболее часто применяемые нечёткие импликации [11] определим
– расширенная по принципу обобщения n-местная t-норма [1]. Используя наиболее часто применяемые нечёткие импликации [11] определим 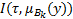 следующим образом:
следующим образом:
- бинарная импликация Клине-Дениса
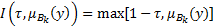 (2.4)
(2.4)
- импликация Лукасевича
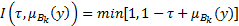 (2.5)
(2.5)
- импликация Райхебаха
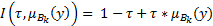 (2.6)
(2.6)
- импликация Фодора
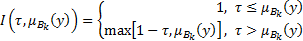 (2.7)
(2.7)
- импликация Решера
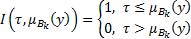 (2.8)
(2.8)
- импликация Гогуена
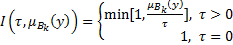 (2.9)
(2.9)
- импликация Геделя
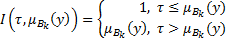 (2.10)
(2.10)
- импликация Егера
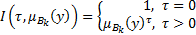 (2.11)
(2.11)
- импликация Заде
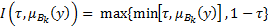 (2.12)
(2.12)
3. Системы нечёткого вывода
Системы нечёткого логического вывода играют важную роль в многочисленных приложениях теории нечётких множеств, таких как нечёткие экспертные системы и многое другие. В основе таких систем лежат логические правила вида «Если …, то …», в которых посылки и выводы являются нечёткими понятиями. Такого рода приближенные рассуждения лежат в основе способности человека понимать естественный язык, распознавать сложные образы, принимать решения в сложной и не полностью определённой среде.
Нечеткий вывод занимает центральное место в нечеткой логике и системах нечеткого управления. Процесс нечеткого вывода представляет собой некоторую процедуру или алгоритм получения нечетких заключений на основе нечетких условий или предпосылок с использованием рассмотренных выше понятий нечеткой логики. Этот процесс соединяет в себе все основные концепции теории нечетких множеств: функции принадлежности, лингвистические переменные, нечеткие логические операции, методы нечеткой импликации и нечеткой композиции. Покажем на рисунке 1 типовую структуру системы нечёткого вывода основанной на нечёткой степени истинности.
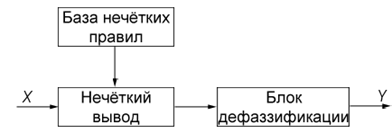
Рис. 1. Структура системы нечёткого вывода, основанной на нечёткой степени истинности
Fig. 1. The structure of the fuzzy system output based on fuzzy truth degree
Покажем на рисунке 2 расширенную структуру системы нечёткого вывода, основанной
на нечёткой степени истинности.
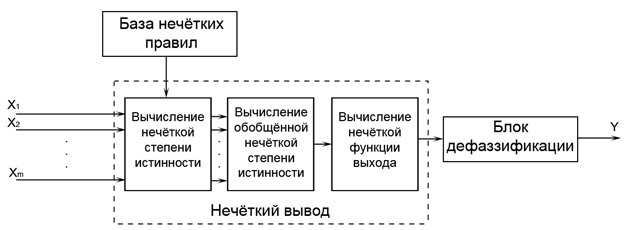
Рис. 2. Расширенная структура системы нечёткого вывода, основанной на нечёткой степени истинности
Fig. 2. Extended structure of the fuzzy system output based on fuzzy truth degree
4. Этапы нечёткого вывода в нечётких системах со многими входами
Процесс вывода, основанный на нечётком значении истинности, исходя из рисунка 2 и [3, 6, 12, 13] может быть выполнен в 3 шага.
Первый предполагает получение нечёткой функции истинности [2, 6] предпосылки, которая непосредственно отражает соответствие факта и предпосылки.
Второй шаг заключается в использовании принципа свёртки нечёткой степени истинности на основе принципа обобщения для получения обобщённой степени истинности.
Третий шаг заключается в получении нечёткой функции выхода с помощью использования композиционного правила вывода в его частном случае – modus ponens.
- Получение нечёткой степени истинности по предпосылке и факту.
Рассмотрим соотношение (2.1). Используя правило истинностной модификации [2, 3], получится:
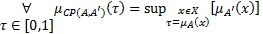 (4.1)
(4.1)
В формуле (4.1) 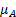 и
и 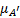 представляют соответственно функцию принадлежности предпосылок и фактов, описанных в универсуме X.
представляют соответственно функцию принадлежности предпосылок и фактов, описанных в универсуме X. 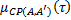 — функция принадлежности нечёткой степени истинности
— функция принадлежности нечёткой степени истинности 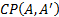 . Другими словами,
. Другими словами, 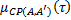 – представляет наибольшее значение X, где
– представляет наибольшее значение X, где 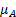 принимает аналогичное значение. Поэтому, получение одного узла кусочно-линейной функции
принимает аналогичное значение. Поэтому, получение одного узла кусочно-линейной функции 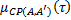 для конкретного значения от
для конкретного значения от 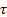 – требует поиска по универсуму X (описывающего узлы
– требует поиска по универсуму X (описывающего узлы 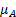 ) и поиска точек, где
) и поиска точек, где 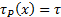 . Далее, анализируются точки
. Далее, анализируются точки 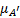 и выбираются их максимумы. Сложность в данном случае, очевидно, линейная и зависит от числа узлов, описывающих
и выбираются их максимумы. Сложность в данном случае, очевидно, линейная и зависит от числа узлов, описывающих 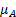 функцию принадлежности. На рисунке 3 показана графическая интерпретация формулы (4.1).
функцию принадлежности. На рисунке 3 показана графическая интерпретация формулы (4.1).
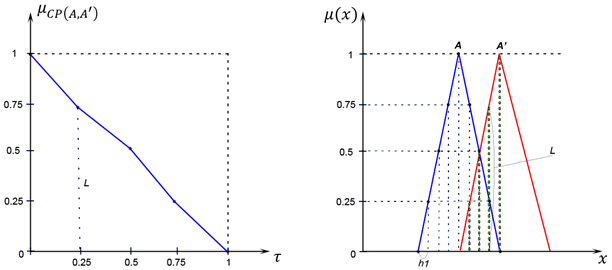
Рис. 3. Графическая интерпретация вычисления по формуле (4.1)
Fig. 3. Graphical interpretation of the calculation according to the formula (4.1)
- Использование принципа свёртки нечёткой степени истинности на основе принципа обобщения
 (4.2)
(4.2)
В выше приведенной формуле  – нечёткая степень истинности составной посылки правила относительно составного факта,
– нечёткая степень истинности составной посылки правила относительно составного факта, 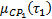 и
и 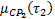 представляют соответственно нечёткую степень истинности первого и второго под условия правила. T – обозначает t-норму, используемую для определения обобщённой нечёткой функции истинности.
представляют соответственно нечёткую степень истинности первого и второго под условия правила. T – обозначает t-норму, используемую для определения обобщённой нечёткой функции истинности.
В наших правилах вида (1.1) присутствуют операции «И» и «ИЛИ» – конъюнкция и дизъюнкция соответственно. Для их вычисления воспользуемся принципом обобщения Заде [9].
Для операции «И» формула (2) примет следующий вид:
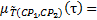
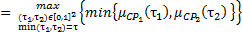 (4.3)
(4.3)
Для операции «ИЛИ» формула (2.5) примет следующий вид:
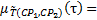
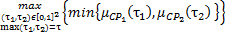 (4.4)
(4.4)
Как видно из вышеприведённых формул (4.3) и (4.4), изменяется t-норма.
- Получение нечёткой функции выхода с помощью использования композиционного правила вывода.
Обобщённый выход получается с помощью модифицированного композиционного правила вывода Заде:
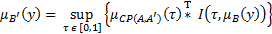 , (4.5)
, (4.5)
где T может быть любой t-нормой.
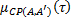 – обобщённая нечёткая степень истинности, вычисляется по формулам (4.3) и (4.4) в результате свёртки сгенерированного нечёткого правила вывода. Выражение (4.5) можно представить в виде композиции:
– обобщённая нечёткая степень истинности, вычисляется по формулам (4.3) и (4.4) в результате свёртки сгенерированного нечёткого правила вывода. Выражение (4.5) можно представить в виде композиции:
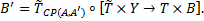 (4.6)
(4.6)
Опишем выражение (4.6) для непрерывного случая, тогда:
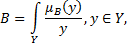
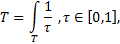
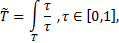
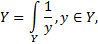
Можно представить выражение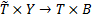 следующим образом:
следующим образом:
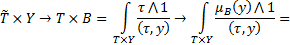
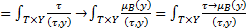 (4.7)
(4.7)
Запишем выражение (4.7) для дискретного случая, получим:
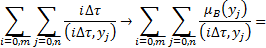
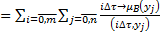 (4.8)
(4.8)
Представим выражение (4.8) в матричной форме:
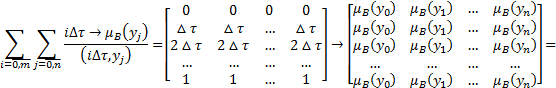
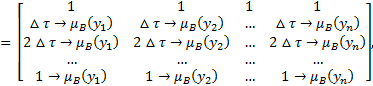 (4.9)
(4.9)
где m – кол-во дискретных точек  , n – кол-во точек базового множества
, n – кол-во точек базового множества 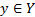 . Результатом выражения (4.9) является матрица размером
. Результатом выражения (4.9) является матрица размером 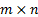 , результатом выражения (4.5) является вектор длины m.
, результатом выражения (4.5) является вектор длины m.
Для вычисления i-того элемента выражения (4.5) воспользуемся следующей формулой:
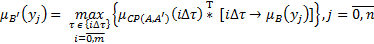 .
.
Если мы используем логическую модель системы и имеем дело с блоком правил, то агрегирование выходов по каждому правилу осуществляется так:
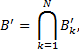
где N – кол-во нечётких правил вывода.
Функция принадлежности 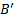 вычисляется с помощью t-нормы:
вычисляется с помощью t-нормы:
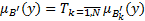 .
.
5. Дефаззификация выхода системы
Дефаззификация в системах нечеткого вывода – это процесс перехода от функции принадлежности выходной лингвистической переменной к её четкому (числовому) значению. Цель дефаззификации состоит в том, чтобы, используя результаты аккумуляции всех выходных лингвистических переменных, получить количественные значения для каждой выходной переменной, которые используется внешними по отношению к системе нечеткого вывода устройствами (исполнительными механизмами интеллектуальной САУ).
Следовательно, данный блок должен осуществить отображение нечёткого множества 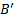 в чёткое скалярное значение
в чёткое скалярное значение 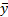 . Используем метод центра тяжести в его дискретном варианте:
. Используем метод центра тяжести в его дискретном варианте:
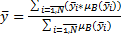 (5.1)
(5.1)
В выражении (6) 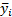 – точка, в которой функция
– точка, в которой функция 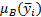 принимает максимальное значение. Если подставить на место
принимает максимальное значение. Если подставить на место 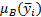 выражение (4.5), то мы получим общую формулу, описывающую нашу систему:
выражение (4.5), то мы получим общую формулу, описывающую нашу систему:
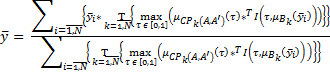 . (5.2)
. (5.2)
6. Тестирование экспертной системы
Пусть имеется бак с водой, который заполняется водой. Пусть подача воды регулируется поворотом крана, который меняет количество пропускаемых литров воды в минуту. Сделаны измерения – предпосылки, покажем их в таблице 1.
Таблица 1
Измерения во время заполнения бака с водой
Table 1
Measurements at the time of filling the tank with water
% поворота крана | Кол-во литров в баке | Пропускная способность крана, литров/мин. |
100 | 0 | 50 |
100 | 0 | 100 |
75 | 0 | 200 |
75 | 50 | 50 |
50 | 100 | 50 |
50 | 100 | 100 |
25 | 150 | 100 |
25 | 100 | 200 |
0 | 200 | 50 |
0 | 200 | 100 |
0 | 200 | 150 |
В результате работы разработанной экспертной системы были получены следующие правила:
- x1 is M2 AND x2 is M1 OR x1 is M2 AND x2 is S THEN d is D2;
- x1 is M2 AND x2 is D1 OR x1 is M1 AND x2 is M1 THEN d is D1;
- x1 is S AND x2 is M1 OR x1 is S AND x2 is S THEN d is S;
- x1 is D1 AND x2 is S OR x1 is S AND x2 is D1 THEN d is M1;
- x1 is D2 AND x2 is M1 OR x1 is D2 AND x2 is S OR x1 is D2 AND x2 is S THEN d is M2;
В выше приведённых правилах введены следующие обозначения:
- % поворота крана – d, выход системы;
- Кол-во литров в баке – x1, первый входной параметр;
- Пропускная способность крана – x2, второй входной параметр;
Для каждого параметра были определены области, в которых они изменяются, покажем их ниже в таблице 2.
Таблица 2
Области для параметров системы
Table 2
Areas for system settings
| Параметр | Области |
| d | M2: [0, 25]; M1: [0, 50]; S: [25, 75]; D1: [50, 100]; D2: [75, 100]; |
| x1 | M2: [0, 50]; M1: [0, 100]; S: [50, 150]; D1: [100, 200]; D2: [150, 200]; |
| x2 | M1: [50, 125]; S: [50, 200]; D1: [125, 200]; |
На вход нашей экспертной системы подаём файл факта, содержащий нечёткие треугольные величины для параметров. Для x1 нечёткая величина определяется следующей тройкой: 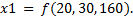 Для x2 нечёткая величина определяется другой тройкой:
Для x2 нечёткая величина определяется другой тройкой: 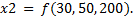
Рассмотрим первое правило:
- x1 is M2 AND x2 is M1 OR x1 is M2 AND x2 is S THEN d is D2;
Данное правило состоит из двух частей, объединённых связкой «OR». Покажем графики нечёткой степени истинности для первой части (x1 is M2 AND x2 is M1) на рисунке 4, а на рисунке 5 результат операции «И».
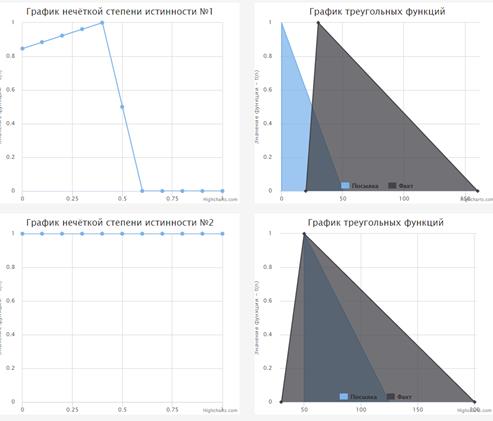
Рис. 4. Графики нечёткой степени истинности для первой части правила
Fig. 4. Charts of odd degree of truth for the first part of the rule
Далее, покажем график объединённой нечёткой функции истинности на рисунке 5.
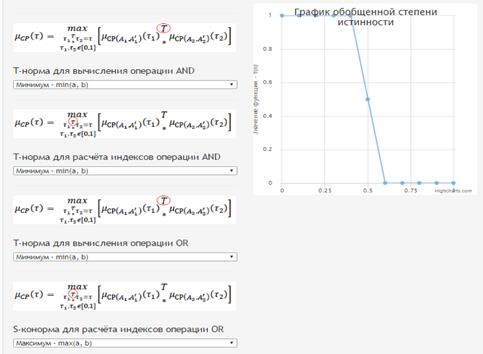
Рис. 5. График объединённой нечёткой функции истинности
Fig. 5. Graph of united fuzzy truth function
Аналогично поступаем для всех остальных правил – найдём нечёткую функцию выхода всех правил для входного факта. С помощью метода центра тяжести (5.1), по формуле (5.2) найдём чёткий выход системы, покажем его на рисунке 6.

Рис. 6. Чёткий выход системы
Fig. 6. A clear system output
Данное число показывает на сколько процентов необходимо повернуть кран, для данных, поступивших на вход системы.
Заключение
В данной статье была описан нечёткий подход, основанный на нечёткой степени истинности для задач нечёткого управления. Была представлена разработанная экспертная система с правилом вывода на основе нечёткой степени истинности. Использование нечёткой степени истинности значительно повышает эффективность решения задач, так как уменьшается сложность алгоритма.
Анализируя дальнейшие возможности и направления продолжения исследований по данной тематике, можно выделить следующие: усовершенствование классических алгоритмов (разработка параллельных алгоритмов). Разработка нечётких экспертных систем является актуальной темой. Поэтому практически обоснованно дальнейшее усовершенствование разрабатываемой системы и увеличение типов, решаемых с помощью нее задач.
















Список литературы
Т. Тэрано, К. Асаи, М. Сугэно. – М.: Мир, 1993. – 368 c.