Введение

При решении задачи восстановления резкости космического изображения высокого разрешения итеративной деконволюцией с различными малыми возмущениями ядра интегрального оператора, реализуется слабоменяющийся от ядра к ядру отклик (в виде результата деконволюции) на регулярные компоненты изображения по сравнению с более выраженной реакцией на стохастические составляющие. Это происходит из-за возрастания аппликат (положительного наклона огибающей) при увеличении пространственных частот в спектральном представлении ядер, т.е. в их пространственно-частотных спектрах (ПЧС) [1-3].

В условиях пересечения ПЧС шумов и тонкой структуры образов объектов, что имеет место на изображениях высокого и сверхвысокого пространственного и спектрального разрешения, задача учета влияния шума и препарирования его на шум и стохастические составляющие тонких структур изображения не решается однозначно. Как правило для препарирования используется факт анизотропии радиуса корреляции стохастической составляющей на линеаменте тонкой структуры. Так как коррекция изображения и сам синтез ядра оператора деконволюции начинается с измерения (адекватного синтеза) функции рассеяния точки (ФРТ) на изображении, то необходимо и целесообразно добиться соотношения энергий регулярных и стохастических компонент на изображении для порождения стохастических составляющих на синтезируемой ФРТ таких, чтоб по энергии они не превышали погрешность итеративного процесса исчисления оператора деконволюции при подавлении той же самой ФРТ (иначе она будет существенно неизопланатичной и вызовет неоднородное распределение уровня коррекций резкости изображения).

Технология нелинейного возмущения оператора деконволюции для препарирования регулярных и стохастических компонент и коррекция резкости на изображении

Естественным шагом для получения изопланатичной ФРТ является обеспечение возможного превалирования регулярных составляющих на изображении над стохастическими [4]. Для этого целесообразно построить следующий верифицирующий процесс:

Операторы деконволюции считаем коррелирующими в зависимости от степени корреляции их ядер, т.е. в зависимости от значения коэффициента корреляции. При этом, если результат работы алгоритма, являющегося вычислимой реализацией оператора, сводится к паре (S_RR,n), где S_RR – регулярная, n – стохастическая составляющие, и для серии алгоритмов L_i, порождающих пары (S_RR,n)_i, построено выражение 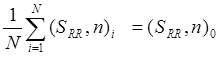, причем норма разницы ||(S_RR,n)₀-(S_RR,n)_i|| ощутимо заметна за счет эволюции n, а не S_RR, отношение сигнал/шум в паре (S_RR,n)₀ улучшилось в 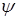раз и нельзя заявить, что 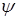<<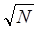, то алгоритмы ансамбля считаем верифицирующими.

В алгоритме L_i обработки входной пары (S_RR,n)_И подвергнем возмущению операцию умножения (возмущая матрицей V_ij малых вещественных значений базовую 10х10-клеточную матрицу, к примеру, операции умножения). Возмущение других операций не рассматривается, отсутствие операции умножения в алгоритмах L_i не предполагается, так как в работе строится общая схема верифицирующих ансамблей для алгоритмов задачи коррекции разрешения, т.е. алгоритмов цифровой фильтрации, деконволюции, ортогональных преобразований. Возмущение считаем малым, если выполняется неравенство

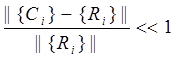                              ,                                          (1)

где ||{C_i}|| и ||{R_i}|| - нормы выходных потоков данных по деконволюции после и до возмущения, соответственно.

Нелинейные возмущения стохастической составляющей искажают ее функцию распределения и расширяют полосу ее спектрального представления [5]. Разным матрицам операции возмущения будут теперь соответствовать стохастические составляющие с разными функциями распределения и несильно возмущенная регулярная составляющая [3]. При выполнении верификации суммированием результирующих пар (S_RR,n)_i, где i – номер матрицы возмущения операции умножения (причем матрицы друг другу не равны), в силу центральной предельной теоремы теории вероятности результирующая стохастическая составляющая будет иметь распределение, близкое к нормальному (при достаточном числе вариантов возмущающих матриц) с соответствующими упомянутой теореме среднеквадратичной дисперсией и математическим ожиданием. Регулярная составляющая в среднем будет нарастать по закону веерного фильтра, а стохастическая составляющая нарастает со значительным отставанием по энергии [3], преобразуясь в нормально распределенную случайную величину [5].

Если 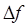 – полоса частотно-контрастной характеристики (ЧКХ) тракта зондирования и 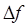<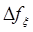, где 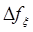 – полоса ПЧС стохастической составляющей после нелинейного возмущения, то в соответствии с теоремой о нелинейном возмущении суммы «сигнал + шум» получим новое соотношение сигнал/шум [5,6]:

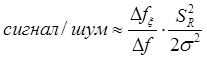,                                                (2)

где 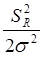 классическое отношение средней энергии слабоизмененной регулярной составляющей на изображении к удвоенной среднеквадратичной дисперсии стохастической составляющей, уменьшенной за сет операции накопления при верификации и нормирования результатов.

На Рис. 1 и Рис. 2 приведены результаты, использующие разнос отклика на возмущенную операцию умножения исходного изображения на единицу на регулярные составляющие и стохастические. В спектральном представлении это разнос отклика на низко-, средне- и высокочастотные составляющие ПЧС изображения. Исходное изображение попиксельно умножалось возмущенной операцией на единицу и вычиталось из исходного. На рисунке 1 (слева) представлено космическое изображение фрагмента городской черты с высоким разрешением, содержащее примерно равнонасыщенные низкие, средние и высшие моды ПЧС. Правее приведены разностные изображения ("возмущенное" минус исходное).

Размещенное в центре рисунка 1 изображение показывает отсутствие регулярной составляющей, т.е. при матрице с нормой 0.05 возмущение регулярной в исходном изображении крайне мало. Изображение, размещенное в правой части показывает наличие на разностном изображении остаточной регулярной составляющей, т.е. матрица с нормой 0.3 в достаточной мере подвергла возмущению и регулярную составляющую на исходном изображении.

Аппроксимируя ЧКХ тракта зондирования для простоты вычислений прямоугольником

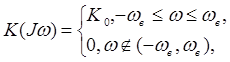                                             (3)

и возбуждая тракт белым шумом с сингулярной функцией автокорреляции (ФАК)

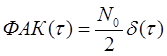,                                            (4)

где 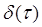  – функция Дирака, получим на выходе тракта шум со спектральной плотностью, равной 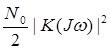. ФАК шума на выходе тракта в соответствии с теоремой Винера-Хинчина [3] будет

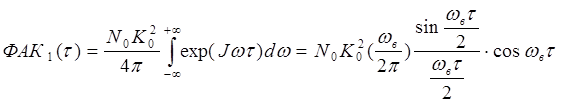,                   (5)

откуда следует, что два любых значения шума при 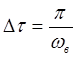 – некоррелированы. На любом окне транспаранта изображения апертурой l будет

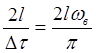                                               (6)

независимых отсчетов шума и 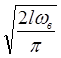 независимых ансамблей для двумерной задачи. Здесь всюду 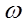- пространственная частота.

Рис. 1. Исходное изображение (слева), разностное с нормой матрицы возмущения 0.05 (в центре), разностное с нормой матрицы возмущения 0.3 (справа)

Fig. 1. Original image (left), difference from the norm of the matrix perturbation 0.05 (center), difference from the norm of the matrix perturbation 0.3 (right)

N разным возмущающим матрицам V_i соответствуют N возмущенных матрицей V_i состояний исходного функционала, удовлетворяющих описанному выше условию реализации откликов на регулярную и стохастическую составляющие. В силу той же эргодической гипотезы число N таких функционалов, слабокоррелирующих, а стало быть порождающих независимые значения случайной величины будет не более 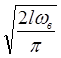. Средние оценки приведенной величины, оцененной для метрических характеристик современных окон формирования космических изображений высокого разрешения дают значение равное примерно .

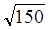На Рис. 2 приведен пример верификации изображения "Город". В верхней части рисунка расположены исходное изображение высокого разрешения (слева) и его спектральный портрет (справа). В средней части рисунка, соответственно, расположены – результат коррекции исходного изображения разработанным методом [3] (опорные ориентиры: фрагмент полосы дороги, отдельные крупные автомобили, центральный дом с прилегающими регулярными компонентами) и его спектральный портрет. В нижней части рисунка, соответственно, расположены – результат верификации на базе описанного выше метода с возмущающими матрицами с нормами 0.05; 0.07; 0.09; 0.11. В соответствии с изложенным выше эффект верификации попиксельным суммированием четырех "возмущенных" изображений измеряется коэффициентом превалирования регулярных компонент равным .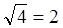

Рис. 2. Исходное изображение и его спектральный портрет (вверху); результат коррекции методом специальной коррекции и его спектральный портрет (в центре); результат верификации и его спектральный портрет (внизу)

Fig. 2. The original image and its spectral portrait (top); the result of correction by the special method of correction and its spectral portrait (center); the result of verification and its spectral portrait (bottom)

На изображении, верифицированном описанном выше способом далее можно ставить и решать задачу более корректного выявления ФРТ по опорному ориентиру и его эталону (при условии нивелирования невязок масштаба, угла места солнца освещения объекта, взаимного поворота и т.д.) [3]. Формирование изображения без учета (или при подавлении) артефактов, вызываемых возмущением СДИ, в модели Бейтса и Мак Доннела представляется в аналитической записи для изображений высокого и сверхвысокого разрешения в виде Фурье-представления интегрального уравнения Фредгольма, связывающего исходное изображение S_R, ФРТ и восстанавливаемое изображение SИ [2]:

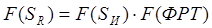                              ,                                          (7)

где ФРТ  является ядром интегрального преобразования (свертки), F(S), F(ФРТ) – Фурье-спектры объектов. Определяемая из (7) для каждого из ОО или полигонных объектов SOO и их эталонов (Э) – S_ИO уникальная ЧКХ тракта в виде

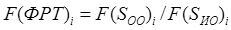                                    (8)

с оценкой F(ФРТ) в виде 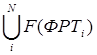 дает оценку искомой ФРТO в виде

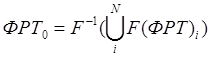.                                               (9)

Нанесение нулевых пикселов на фрейм для выявления самого ОО из фона – это задача корректного определения контуров, обрамляющих ОО, иначе в процессе определения ФРТ будут участвовать и пикселы фона. Целесообразно это реализовать веерными фильтрами [3].

Анизотропия радиуса корреляции линеамента образа объекта антропогенного происхождения в отличие от радиуса корреляции шума делает веерный фильтр особенно чувствительными к отклонению азимута фильтрации, т.е. к отклонению направления простирания границы образа объекта, что повышает профит фильтра, а для криволинейных границ или контуров эффект фильтрации сохраняется при многократном запуске фильтра, но с малой базой, соответствующей разложению участка кривой в соответствии с алгоритмом Брезенхейма или переходом к Фурье-представлению веерной фильтрации [3]. На рисунке 3 приведены исходное тестовое изображение, зашумленное изображение и сравнительные результаты исследования веерного фильтра.

Рис.3. Слева направо: исходное тестовое изображение; зашумленное равнораспределенным нормальным шумом исходное тестовое изображение (соотношение сигнал/шум=0.8); далее результаты обработки зашумленного тестового изображения: фильтром Винера, линейным матричным фильтром с нормализацией, линейным фильтром в частотной области с обнулением кольца пространственных частот с номерами выше 50, адаптивным фильтром графического пакета PHOTOPAINT, веерным фильтром с параметрами: количество проходов – 2, длина базы – 17 и 5, количество направлений – 36

Fig.3. Left to right: original test image; evenly suspended noise normal noise source test image (the ratio signal/noise=0.8); further, the results of processing a noisy test image: a Wiener filter, linear matrix filter with the normalization, a linear filter in the frequency domain by zeroing ring of spatial frequencies with numbers above 50, the adaptive filter graphic package PHOTOPAINT, fan filter with the following parameters: number of passes – 2, the length of the base 17 and 5, the number of directions is 36

Для выделения ОО на приведенных ниже материалах с аппарата OrbView-3 – самолете на стоянке и его эталоне – более резком изображении, выделялись для корректного оконтуривания опорного ориентира (и эталона) компоненты изображений – локальные спектральные максимумы в выделенных участках спектра фрейма с объектом. Далее находился энергетический максимум результатов веерной фильтрации в разных базах фильтрации, не выходящих по величине за пределы соотношения неопределенности для данной выделенной полосы. Полный портрет ОО и эталона реализовался операцией объединения обработанных участков спектра и обратным Фурье преобразованием [3].

На рисунке 4 можно видеть эталон и соответствующий опорный ориентир с устраненными взаимными невязками геометрии, масштаба, угла поворота, гистограммы. Они выбраны на соответствующих паттернах изображения и отфильтрованы от фона, помещены в рабочий фрейм и приведены к виду, инвариантному к углу места солнца.

Рис.4. Слева направо: эталон и соответствующий опорный ориентир с устраненными взаимными невязками, выбранные на соответствующих паттернах изображения и отфильтрованные от фона; далее эталон и соответствующий опорный ориентир, помещенные в рабочий фрейм и приведенные к виду инвариантному к углу места солнца

Fig.4. Left to right: the reference and the corresponding reference point with fixed mutual residuals, selected on the corresponding patterns of the image and filtered from the background; then the reference and corresponding reference point, placed in the working frame and reduced to the form invariant to the elevation angle of the sun

Коэффициент корреляции ОО и Э не может быть равен 1, иначе ОО и Э идентичны и тогда нет постановки задачи, ниже 0.7 – запрещенные значения, т.к. отсутствует при этом возможность доказать что это сопряженная пара ОО и Э. Следует сделать оговорку: значение коэффициента корреляции, допустим, 0.7, а распознавание ОО и идентификация его соответствия эталону должна сопровождаться уровнем ложной тревоги не выше 0.1, т.е. распознавание и идентификация выполняются при дополнительных признаках [6]. Например, наблюдаемый ОО – самолет, тогда его можно сравнивать только с эталоном самолета F105R, и выяснить, к примеру, что на отслеживаемом аэродроме других не бывает. В F(ФРТ_O), которое и порождает инверсные и Винеровские фильтры с модификациями, включая модификации на частотно-зависимую добавку [7 каждая i,j-ая мода характеризуется значением функции принадлежности µ_0ij, определенной по выше описанному правилу для (3), и строилась она на значениях коэффициентов корреляции эталонов и ОО.

Значение взвешенной суммы вида

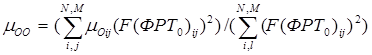                              (10)

где 0.7 <= µ₀₀< 1 целесообразно принять за достоверность F(ФРТ_O) и ФРТ_O.

По вычисленной µ₀₀  определим разброс 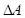 апертур ФРТ, используя множитель вида 1-µ₀₀  на расширение и сужение выявленной апертуры A(ФРТ):

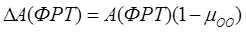.                                          (11)

При ФРТ этом интерполируется на новые апертуры с сохранением ее энергии (суммы квадратов аппликат).

Далее выполняется специальная коррекция резкости (СКР) в соответствии с техникой, представленной в работах[1,7], с пошаговым малым наращиванием «заниженной» апертуры ФРТ до остановки процесса роста резкости на каждом шаге и СКР с пошаговым малым уменьшением «завышенной» апертуры ФРТ до появления на каждом шаге отмеченных в [1] артефактов в виде паразитного контрастирования.

Необходимо заметить, что монотонность в пошаговом наращивании или уменьшении апертур ФРТ на запуск итераций порождает монотонность тенденции изменений резкости, получаемой при заданной погрешности итеративных процессов, но дисперсия отклонений получаемых резкостей от оси выявленной тенденции может превышать указанную погрешность. Анализ соотношений (7), (8) и (9), как базовой модели коррекции резкости наводит на вывод, что «всплески» резкости на фоне тенденции изменения при принятом алгоритме построения последовательности ФРТ с сохранением ее энергии определяются (в первом приближении) уровнем энергии частоты в изображении, совпадающей со средневзвешенной модой в ПЧС используемой в данный момент ФРТ.

При монотонном переборе значений апертур ФРТ с увеличением их и уменьшением, как описано выше, из-за нестойкой монотонности получаемых результатов по деконволюции приходится на этих результатах вводить меру получаемой резкости - Лебега (внешнюю и внутреннюю), а окончательную оценку резкости искать на интервале несовпадения внешней и внутренней меры.

Все процессы СКР завершаются итеративным представлением Ван Циттера, а формула погрешности итерационного процесса имеет вид [7]:

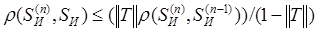,                                 (12)

где 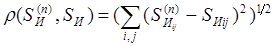 – евклидова метрика, а  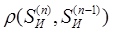исчисляется аналогично; норма оператора Т в соответствии с технологией СКР равна

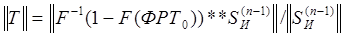,                                      (13)

где числитель и знаменатель – евклидова норма (формула Пифагора) на компонентах векторов. Легко заметить, что понимание ФРТ при верификации регулярных компонент изображения как изопланатичной ФРТ определится из условия достижения при верификации разницы норм регулярной ||S_RR|| и стохастической ||S_RS|| компонент изображения абсолютного заданного значения погрешности исчисления оператора деконволюции.

||S_RR||-||S_RS||=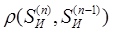                                             (14)

Ниже, на рисунке 5 приведен результат с более высоким значением резкости, полученный в описываемой технологии учета ошибок определения ФРТ и фильтрацией шума с введением меры Лебега для резкости в соответствии с технологией, представленной в [7], с расширением числа ОО, выбранных на исходном снимке. В последовательности итеративных деконволюций полученный результат стоит после последней итерации в предыдущей версии коррекции резкости [7] и перед наступающим срывом корректности в коррекции резкости в предыдущей версии.

Рис.5. Слева направо: результат СКР, результат с учетом ошибок по ФРТ, результат срыва корректности работы СКР на последующей итерации в СКР

Fig.5. Left to right: the result TFR result of the accounting errors on the TRF, is the result of disruption of correct operation of the RCDS on a subsequent iteration in the TFR

Получаемый экстремальный по резкости результат при выполнении верификации в СКР проявлялся на 10-15 итераций раньше, чем при выполнении СКР без верификации на нелинейных возмущениях оператора деконволюции

Заключение

Разработан метод корректировки результатов функционирования итеративного интегрального оператора деконволюции исходного изображения по оценке достоверности функции рассеяния точки, композируемой из функций рассеяния, определяемых по опознанным опорным ориентирам; метод разработан как модернизация представленной ранее специальной коррекции резкости на изображениях высокого разрешения с применением предварительного построения верифицирующего набора регулярных составляющих на изображении.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 14-07-00171 "Разработка теоретических основ методов моделирования и алгоритмов представления в обобщенных операциях трактов преобразования дистанционных данных с максимизацией эффективности обработки информации (цифровых космических изображений)" и научного проекта № 16-07-00177 "Разработка теоретических основ методов моделирования реализации предельно достижимых характеристик сверхвысокого пространственного и спектрального разрешения в стволах дистанционного зондирования с космических платформ"