О МЕТОДЕ ОПТИМАЛЬНОЙ СУБПОЛОСНОЙ ФИЛЬТРАЦИИ
Aннотация
В данной работе изложены результаты экспериментальных исследований эффективности применения метода оптимальной субполосной фильтрации, обеспечивающего минимальный уровень просачивания энергии за пределы выбранной для фильтрации подобласти пространственных частот. В ходе экспериментов показано, что энергия входного изображения, сосредоточенная вне выбранной подобласти пространственных частот, влияет на выходную частотных фильтров, основанных на применении ДПФ, в значительно большей степени, чем на результат, полученный на основании метода оптимальной фильтрации. Данное влияние проявляется как на графиках значений соответствующих трансформант Фурье, так и на изображениях, полученных в результате фильтрации.
Ключевые слова: изображение, оптимальная фильтрация, трансформанта Фурье, подобласть пространственных частот
Введение
Одно из направлений интенсивного развития современных информационно-телекоммуникационных систем определяется тенденцией использования наиболее естественных для человека форм информационного обмена, и, прежде всего, в виде визуальных данных. Обработка изображений является важной задачей. Существующие в настоящее время методы выделения (фильтрации) значимых характеристик отдельных компонент изображения, некоторых периодических структур изображений не являются оптимальными с точки зрения аппроксимации трасформант Фурье в заданной подобласти пространственных частот (ППЧ), в которых осуществляется фильтрации. Поэтому актуальной проблемой является создание математических моделей и методов фильтрации, позволяющих адекватно учитывать энергетические характеристики изображений в выбранной подобласти пространственных частот. В работе [1] разработан и теоретически обоснован новый метод оптимальной линейной фильтрации изображений на основе частотных представлений, который является оптимальным в том смысле, что спектр получаемого в результате фильтрации изображения имеет наименьшее среднеквадратическое отклонение от спектра фильтруемого изображения в заданной двумерной подобласти пространственных частот, а вне этой подобласти пространственных частот имеет наименьшее отклонение от нуля. В работе представлены результаты экспериментальных исследований эффективности метода оптимальной фильтрации изображений на основе частотных представлений в заданной подобласти пространственных частот на примере модельных изображений.
Теоретические основы метода оптимальной фильтрации изображений на основе частотных представлений
О частотных представлениях при обработке изображений [2] можно говорить, поскольку изображение, как функция с конечной или неограниченной областью определения, может быть представлено в виде суммы синусов и косинусов различных частот, умноженных на некоторые весовые коэффициенты
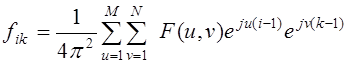 , i = 1,2,…,M, k= 1,2,…,N, (1)
, i = 1,2,…,M, k= 1,2,…,N, (1)
где F(u,v) – значение трансформанты Фурье функции
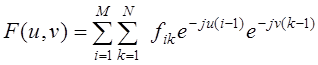 , u = 1,2,…,M, v= 1,2,…,N. (2)
, u = 1,2,…,M, v= 1,2,…,N. (2)
Метод оптимальной фильтрации изображений на основе частотных представлений [1,3] позволяет для нахождения результатов 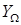 фильтрации изображения Ф=(fik), i=1,2,…,M, k=1,2,…,N, в частотной двумерной области
фильтрации изображения Ф=(fik), i=1,2,…,M, k=1,2,…,N, в частотной двумерной области 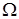 построить вычислительную процедуру, не вычисляя при этом трансформанту Фурье. Для фильтрации изображений предложено использовать следующий вариационный принцип: трансформанта Фурье Z(u,v) результата фильтрации
построить вычислительную процедуру, не вычисляя при этом трансформанту Фурье. Для фильтрации изображений предложено использовать следующий вариационный принцип: трансформанта Фурье Z(u,v) результата фильтрации 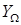 , является оптимальной в смысле евклидовой нормы ее отклонения в заданной подобласти пространственных частот
, является оптимальной в смысле евклидовой нормы ее отклонения в заданной подобласти пространственных частот 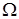 от трансформанты Фурье F(u,v) исходного изображения Ф и от нуля – вне данной ППЧ, т.е.
от трансформанты Фурье F(u,v) исходного изображения Ф и от нуля – вне данной ППЧ, т.е.
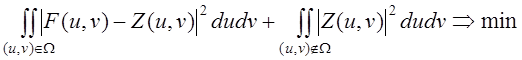 . (3)
. (3)
Указанному вариационному принципу соответствует следующее изображение 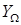
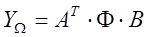 , (4)
, (4)
где матрицы A=(ai1i2), i1,i2=1,2,…,M, и B=(bk1k2), k1,k2=1,2,…,N (субполосные матрицы [2]), определяются соотношениями
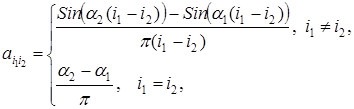
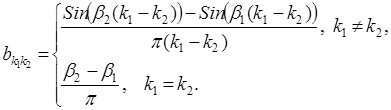 (5)
(5)
Значения
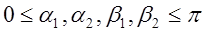 (6)
(6)
задают границы подобласти пространственных частот 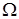 .
.
Важным свойством определенного таким образом результата фильтрации является то, что указанный метод не допускает растекания энергии двумерного сигнала за пределы заданной частотной области.
Концептуальные основы экспериментальных исследований
В ходе вычислительных экспериментов проводился сравнительный анализ оценки доли энергии изображения 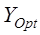 , полученного в результате оптимальной фильтрации,
, полученного в результате оптимальной фильтрации,
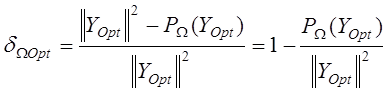 , (7)
, (7)
где 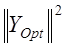 –энергия изображения
–энергия изображения 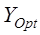 в области определения трансформанты Фурье,
в области определения трансформанты Фурье,
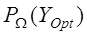 – доля энергии изображения
– доля энергии изображения 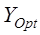 в подобласти пространственных частот
в подобласти пространственных частот 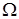 , определяемая на основании соотношения
, определяемая на основании соотношения
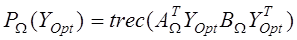 . (8)
. (8)
с соответствующими характеристиками изображений, полученных при реализации известных частотных фильтров [4]:
– идеальный фильтр (результат фильтрации YIdeal),
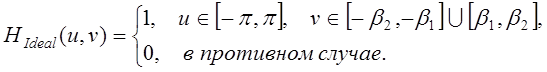 (9)
(9)
– фильтр Баттерворта порядка n=2 (результат фильтрации YButterw),
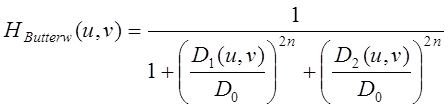 , (10)
, (10)
где D0 – частота среза, D1(u,v), D2(u,v) – расстояние между точкой (u,v) и осями симметрии l1, l2 фильтра,
– Гауссов фильтр (результат фильтрации YGaussian),
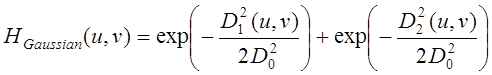 , (11)
, (11)
где D0 – частота среза, D1(u,v), D2(u,v) – расстояния между точкой (u,v) и осями симметрии l1, l2 фильтра.
Построение фильтров осуществлено на основании параметров подобласти пространственных частот, в которой выполнялась оптимальная фильтрация [5,6].
Соответствующие оценки доли энергии результатов фильтрации (изображения YIdeal, YButterw, YGaussian), которая сосредоточена вне выбранной подобласти пространственных частот 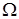 , имеют следующий вид
, имеют следующий вид
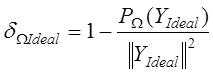 , (12)
, (12)
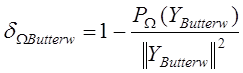 , (13)
, (13)
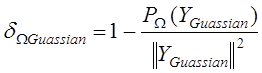 . (14)
. (14)
Отметим, что вычисления как относительной доли «просачивания» энергии за пределы подобласти пространственных частот оказались доступными, благодаря разработанному в [1] методу вычисления долей энергии (8).
Для получения большей наглядности при оценивании различий оптимальной фильтрации и фильтрации c помощью известных фильтров представляется естественным построить графики соответствующих характеристик выходных последовательностей фильтров.
Сравнительный анализ в работе выполнен, исследуя параметры фильтров и результаты их применения в различных подобластях двумерной области (подобласти получены при фиксированных значениях одной из независимых переменных частотного пространства). Однако, данный факт не снижает важности полученных результатов в виду известного свойства преобразования Фурье (преобразование Фурье можно записать так, что переменные в нем оказываются разделенными).
Результаты вычислительных экспериментов
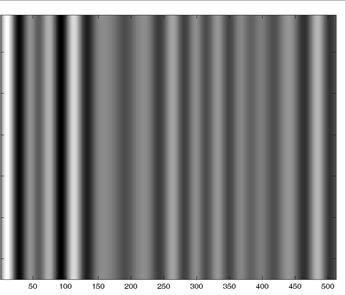
Экспериментальные исследования целесообразно осуществлять на основе обработки модельных сигналов. Генерирование значений модельного изображения (рис. 1) 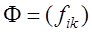 , i = 1,2,…,512, k= 1,2,…,512, размерностью 512х512 пикселей, осуществляется на основе соотношения
, i = 1,2,…,512, k= 1,2,…,512, размерностью 512х512 пикселей, осуществляется на основе соотношения
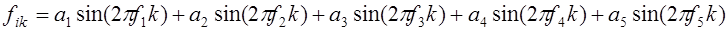 , (15)
, (15)
i = 1,2,…,512, k= 1,2,…,512,
где
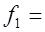 0.0193;
0.0193; 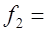 0.0208;
0.0208; 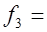 0.0279,
0.0279, 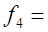 0.0295,
0.0295, 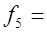 0.0311,
0.0311,
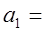 3.2;
3.2; 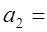 2.9;
2.9; 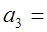 3.5,
3.5, 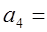 2.1,
2.1, 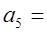 2.2.
2.2.
Такие значения частот позволяют осуществить исследование различных аспектов фильтрации и, прежде всего, влияний энергии исходного сигнала за пределами подобласти пространственных частот на ее результаты.
Фильтрация модельного сигнала (15) на основании метода оптимальной фильтрации изображений на основе частотных представлений осуществлялась в следующей подобласти пространственных частот:
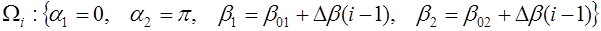 , i=1,2,…,15, (16)
, i=1,2,…,15, (16)
где 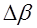 – величина смещения границ очередной ППЧ.
– величина смещения границ очередной ППЧ.
а б
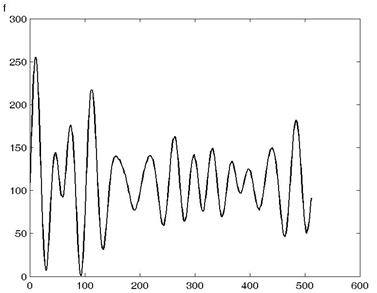
Рис. 1. Модельное изображение: а – в виде изображения, б – профиль
Fig. 1. Model image: a – in the form of images, b – profile
В ходе экспериментов были использованы следующие значения границ подобласти пространственных частот
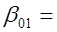 0.035
0.035 ,
, 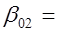 0.04
0.04 ,
, 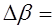 0.0025
0.0025 . (17)
. (17)
В таблице представлены значения долей энергии выходных последовательностей оптимального и других анализируемых фильтров, находящихся вне заданной подобласти пространственных частот, вычисленные согласно (7), (12)-(14).
Как показано в ходе экспериментов выходная последовательность оптимального фильтра определяется только трансформантой Фурье в выбранной подобласти пространственных частот. В отличие от этого, на выходную последовательность идеального, Гауссова фильтров и фильтра Баттерворта влияет энергия входного изображения, сосредоточенная вне выбранной подобласти пространственных частот. Это различие легко обнаружить на рис. 2, на котором представлены абсолютные значения трансформант Фурье выходных последовательностей оптимального и других фильтров.
Таблица 1
Оценка долей энергии результатов фильтрации вне подобласти пространственных частот 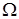
Table 1
Estimation of the energy share of filtered results outside the subdomain of spatial frequencies 
№ | Границы ППЧ 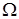 | 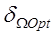 | 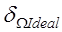 | 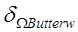 | 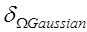 | |
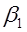 | 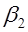 | |||||
1 | 0.035  | 0.04  | 0.13211 | 0.28323 | 0.27313 | 0.27189 |
2 | 0.0375  | 0.0425  | 0.3492 | 0.30822 | 0.31119 | 0.31036 |
3 | 0.04  | 0.045  | 0.13101 | 0.55406 | 0.55503 | 0.55472 |
4 | 0.0425  | 0.0475  | 0.34099 | 0.72638 | 0.55996 | 0.60419 |
5 | 0.045  | 0.05  | 0.41356 | 0.86981 | 0.87022 | 0.87001 |
6 | 0.0475  | 0.0525  | 0.23196 | 0.56816 | 0.57263 | 0.57082 |
7 | 0.05  | 0.055  | 0.34246 | 0.58755 | 0.6305 | 0.62484 |
8 | 0.0525  | 0.057  | 0.12423 | 0.22294 | 0.22436 | 0.22396 |
9 | 0.055  | 0.06  | 0.33214 | 0.63152 | 0.6312 | 0.63129 |
10 | 0.0575  | 0.0625  | 0.40426 | 0.85964 | 0.7762 | 0.8095 |
11 | 0.06  | 0.065  | 0.1968 | 0.41986 | 0.4204 | 0.42016 |
12 | 0.0625  | 0.0675  | 0.24863 | 0.57319 | 0.57095 | 0.57158 |
13 | 0.065  | 0.07  | 0.4328 | 0.92163 | 0.92157 | 0.92155 |
14 | 0.0675  | 0.0725  | 0.47163 | 0.69156 | 0.69313 | 0.69208 |
15 | 0.07  | 0.075  | 0.20767 | 0.7969 | 0.68474 | 0.7815 |
Далее представлены результаты фильтрации модельного изображения (рис. 1) в подобласти пространственных частот
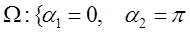 ,
, 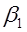 = 0.04
= 0.04 ,
, 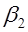 = 0.045
= 0.045 }.
}.
На рис. 2 приведены абсолютные значения трансформант Фурье при u=0.22 , vÎ[0.03
, vÎ[0.03 , 0.075
, 0.075 ] исходного изображения и результатов фильтрации, полученных при применении оптимального и других фильтров в заданной подобласти пространственных частот
] исходного изображения и результатов фильтрации, полученных при применении оптимального и других фильтров в заданной подобласти пространственных частот 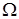 .
.
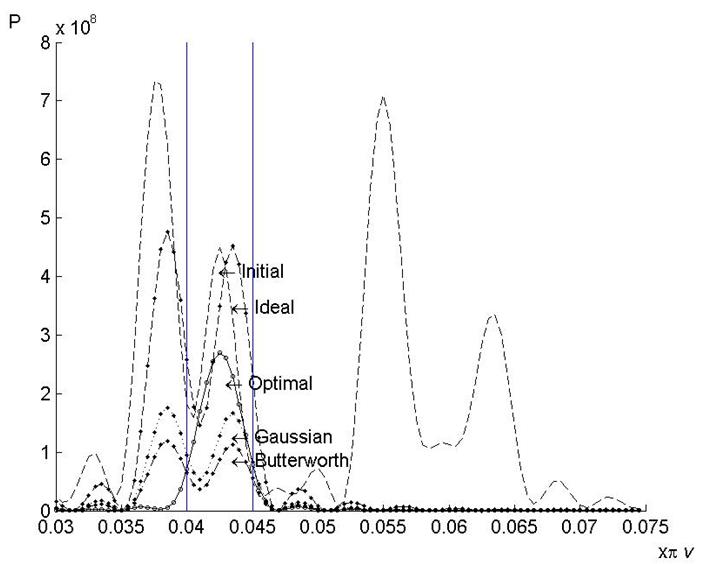
Рис. 2. Трансформанты Фурье (абсолютные значения) в подобласти пространственных частот a1=0, a2= ,
, 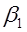 =0.04
=0.04 ,
, 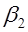 =0.045
=0.045 при u=0.22
при u=0.22 :
:  – исходного изображения; выходных последовательностей фильтров:
– исходного изображения; выходных последовательностей фильтров:  – оптимальный,
– оптимальный,  – идеальный,
– идеальный,  – Баттерворта,
– Баттерворта,  – Гауссов
– Гауссов
Fig. 2. Fourier transforms (absolute values) in a subdomain of spatial frequencies a1=0, a2= ,
, 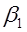 0.04
0.04 ,
,  =0.045
=0.045 при u=0.22
при u=0.22 :
:  - original image; output sequences of filters:
- original image; output sequences of filters:  – optimal,
– optimal,  – ideal,
– ideal,  – Butterworth,
– Butterworth,  – Gaussian
– Gaussian
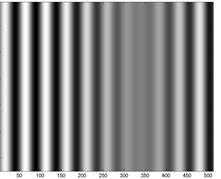
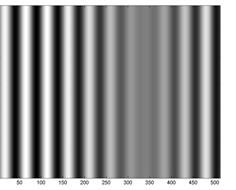
На рис. 3 влияние дополнительной энергии исходного изображения, сосредоточенной вне выбранной подобласти пространственных частот у ее левой границы (рис. 2), проявляется в наличии существенных изменений яркости пикселей изображений (рис. 3в, 3д, 3ж), являющихся результатами фильтрации с помощью фильтров, отличных от оптимального фильтра, и в наличии биений на графиках соответствующих профилей изображений.
 а
а 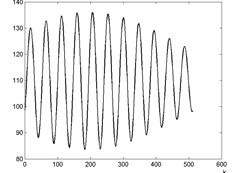 б
б
 в
в 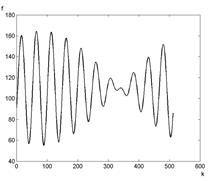 г
г
 д
д 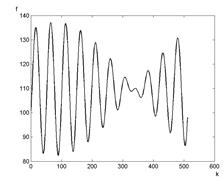 е
е
 ж
ж 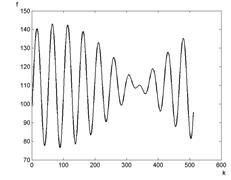 з
з
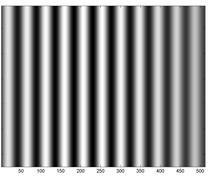
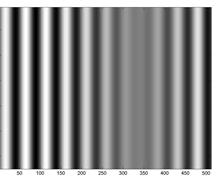
Рис. 3. Результаты фильтрации (изображение и профиль) на основании фильтров: а, б – оптимальный; в, г – идеальный; д, е – Баттерворта, ж, з – Гауссов
Fig. 3. The filter results (image and profile) based on the filters: a, b – optimal; с, d – ideal; e, f Butterworth; g, h – Gaussian
Выводы
Результаты вычислительных экспериментов как с модельными изображениями, так и с реальными фотоснимками в цифровом виде показывают, что относительные доли «просачивания» энергии за пределы указанной подобласти пространственных частот у выходных последовательностей частотных фильтров, основанных на применении ДПФ, существенно больше, чем у разработанного метода.
В ходе экспериментов показано, что энергия входного изображения, сосредоточенная вне выбранной подобласти пространственных частот, влияет на выходную частотных фильтров, основанных на применении ДПФ, в значительно большей степени, чем на результат, полученный на основании метода оптимальной фильтрации. Данное влияние проявляется как на графиках значений соответствующих трансформант Фурье, так и на изображениях, полученных в результате фильтрации.
Работа выполнена при поддержке гранта РФФИ 15-07-01570 (Субполосная скрытная интеграция/извлечение дополнительной информации в аудио или видео контентах).
















Список литературы