Функционирование любой информационно-образовательной среды (ИОС) вуза, реализованной на аппаратно-программной платформе вычислительной системы с распределенной обработкой данных (СРОД) может быть представлено в виде совокупности взаимодействий пользователей (обучаемых, педагогов, других сотрудников) с системой [1,2]. С формальной точки зрения любое такое взаимодействие можно отобразить в виде последовательности этапов передачи и обработки информации.

Для оценки взаимодействия однородных информационных процессов (ИП) в вычислительной подсистеме ИОС предлагается подход, основанный на агрегативном описании систем с использованием особенностей их структуры.

Существо подхода заключается в выделении из рассматриваемой системы некоторой подсистемы (агрегата) и последующем ее детальном исследовании; при этом учитывается влияние остальной части системы, которая представляется в виде обобщенной сети массового обслуживания (СМО) с интенсивностью обслуживания, зависящей от числа заявок в ней.

Полагается, что эта СМО ведет себя по отношению к оставшейся подсистеме аналогично той части системы, которую она заменяет.

В общем случае СРОД достаточно сложной структуры может быть разбита на несколько подсетей, которые исследуются отдельно. При этом объединение отдельных СМО в подсети осуществляется таким образом, чтобы:

– взаимодействия элементов внутри подсети (внутренние взаимодействия) могли быть исследованы без учета;

– взаимодействий между подсетями; взаимодействия между подсетями (внешние взаимодействия) можно было анализировать без учета внутренних взаимодействий.

Указанные условия будут выполняться, если частота внутренних взаимодействий много больше частоты внешних взаимодействий. В этом случае говорят о почти разложимой системе.

Агрегативные модели дают точное решение для сетей, допускающих решение в виде произведения. Так можно показать, что точное решение может быть получено для сетей МО, описываемых моделью Гордона – Ньюэлла [3]. Агрегативный подход часто связывают с замкнутыми сетями, однако он может быть использован и в отношении открытых сетей МО.

Рассмотрим функционирование вычислительного комплекса (ВК) в режиме реального масштаба времени, ограничиваясь анализом ИП на уровне ВК. Пусть на ВК поступает пуассоновский поток заявок интенсивностью λ, а реализуемые информационно-вычислительные работы (ИВР) связаны с выполнением достаточно длинной цепочки переходов: процессор–внешнее устройство- процессор…. Время обслуживания одного запроса на устройство  распределено по экспоненциальному закону со средним 1/μ_j. Здесь индекс «1» относится к узлу процессора. Вероятность выхода на узел (устройство) 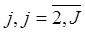, после обслуживания в узле процессора есть θ_1j. Наибольший допустимый уровень мультипрограммирования в вычислительном комплексе – N.

Для исследования ИП в подобной ситуации может быть использован как аппарат открытых, так и замкнутых сетей МО. Однако в первом случае не будет учитываться ограничение на уровень мультипрограммирования, что может привести к существенному завышению оценок пропускной способности вычислительного узла, особенно при большой загрузке системы. Во втором случае получаемые оценки будут занижены, поскольку при расчетах будет приниматься максимальная пропускная способность вычислительного комплекса, соответствующая уровню мультипрограммирования N, в то время как при числе активных ИП в вычислительном узле, меньшем N, эта величина может заметно отличаться от ее максимального значения.

В данной ситуации ошибка в расчетах увеличивается с уменьшением загрузки системы. Для преодоления указанных трудностей необходима модель, отражающая реальную зависимость пропускной способности рабочей станции от числа активных ИП. Такая модель получается при использовании агрегативного подхода. В самом деле, интенсивность переходов между состояниями, связанными с занятием отдельных ресурсов (процессоров, ВУ) при реализации активного ИП, значительно больше интенсивности последовательных активизаций ИП. Поэтому можно выделить и рассмотреть отдельно замкнутую подсеть, отображающую процесс реализации в мультипрограммном режиме n активных ИП, .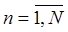

На рис. 1. а схематически представлена рассматриваемая открытая сеть МО, а на рис. 1,б – образованная из нее подсеть, которую условно можно считать замкнутой.

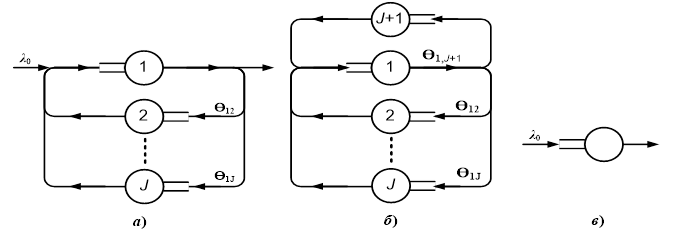
Рис. 1. Агрегирование открытой сети МО

Fig. 1. Aggregation of an open queuing network

В последнем случае для удобства вычислений введен фиктивный узел J+1, для которого полагаем 1/μ_J+1=0.

Пропускная способность вычислительного комплекса определяется зависимостью 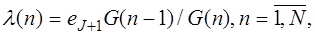(1)

                                                                                                                (1)

т.е. является функцией от n. При этом e_J+1 определяется решением системы:

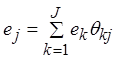, a G(K) рассчитывается по рекуррентной формуле

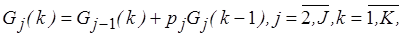                                                                                                (2)

где К – число заявок, циркулирующих в сети.

Рассмотренную подсеть заменим эквивалентным обслуживающим прибором, интенсивность обслуживания которым выражается следующим образом:

                                                                                                         (3)

Допуская теперь, что время обслуживания эквивалентным прибором можно считать распределенным по экспоненциальному закону, рассматриваемую систему представим в виде СМО типа M/M/1 с переменной интенсивностью обслуживания, задаваемой соотношением (3). Решение такой СМО может быть записано в виде:

                                                                                                        (4)

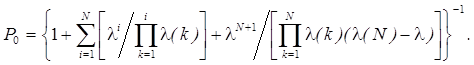
Рассчитав стационарные вероятности состояний (4), можно получить требуемые характеристики реализации ИП в системе. Например, среднее число заявок в системе выразится как

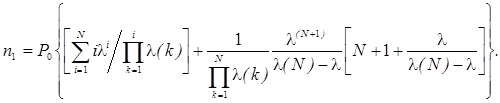
Отсюда среднее время реакции рабочей станции определяется на основании формулы Литтла: .

Рассмотрим пример, демонстрирующий основные особенности расчетных схем рассматриваемой модели.

Пусть необходимо оценить пропускную способность ВК, схематически изображенного на рис. 2, где показана его структура: процессор (узел 1) и три внешних запоминающих устройства (ВЗУ) (узлы 2, 3, 4). Каналы обмена данными в ВК не являются узким местом, так что очереди образуются лишь к процессору и ВЗУ. Объем оперативной памяти ВК такой, что возможна одновременная реализация лишь двух ИП (работа в двухпрограммном режиме). Параметры соответствующих ИП заданы; время одного обслуживания любым из устройств можно считать распределенным по экспоненциальному закону с интенсивностями 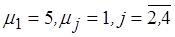; после завершения обслуживания процессором с равной вероятностью 0,3 выдаются запросы на устройства 2, 3,4 и с вероятностью 0,1 ИП завершается.

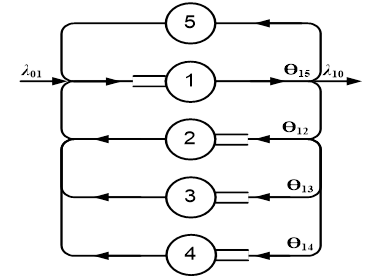
Рис. 2. Пример структуры ВК

Fig. 2. An example of the structure of a computing system

При сравнении оценок основных характеристик реализации, полученных на основе агрегативного подхода, будем полагать, что пропускная способность рабочей станции определяется как λ(N). Для простоты будем полагать, что предельный уровень мультипрограммирования N=2. Результаты расчетов представлены в табл. 1, где приведены значения среднего числа ИП в системе (N1) и среднего времени реакции рабочей станции(υ₁).

Таблица 1

Результаты вычислительного эксперимента с различными типами моделей

Table 1

The results of computational experiments with various types of models

λ	Замкнутая модель		Агрегативная модель		Открытая модель
	N1		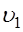N1		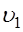N1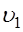
0,05	0,5	10	0,68	13,4	0,65	13
0,1		20	2,3	23	0,69	6,9
0,14		93	14,3	102	2,6	18
0,2	-	-	-	-	4,8	24
0,33	-	-	-	-	299	906

Анализируя эти данные, можно обратить внимание, что при малой загрузке рабочей станции (малых значениях входящего потока заявок на ИВР) результаты расчетов, полученные на основе агрегативного подхода и в результате анализа открытой сети МО, весьма близки. Это вполне естественно, поскольку в данном случае система работает с недогрузкой и ограничение на уровень мультипрограммирования почти не проявляется. При большой загрузке системы 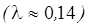 оценки, полученные на основе агрегативного подхода, близки к соответствующим оценкам, полученным путем анализа замкнутой сети МО 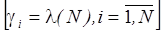. Этот факт также легко объясняется: в условиях большой загрузки система почти постоянно работает при максимальном уровне мультипрограммирования, что соответствует наивысшей пропускной способности. Таким образом, использование агрегативного подхода в данном случае позволяет наиболее полно отобразить реальные условия функционирования ВК.

Аналогичным образом агрегатирование применимо и при исследовании замкнутых систем. Рассмотрим в качестве примера ВК, обслуживающий некоторое число M абонентов, каждый из которых обращается к рабочей станции с заявками на ИВР [4].

Время между последовательными обращениями абонента к рабочей станции распределено по экспоненциальному закону с параметром λ. Причем новая заявка может быть сформирована абонентом лишь после получения ответа на предыдущую. Следовательно, при наличии в рабочей станции(на обслуживании и в очереди) i заявок поток заявок от всех абонентов будет иметь пуассоновский характер с интенсивностью

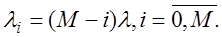                                                                                     (5)

Пусть наибольший уровень мультипрограммирования для рабочей станции есть N.

Теперь, рассматривая рабочую станцию как замкнутую сеть МО, можем, как и ранее, определить величины λ(n) в соответствии с (1). Предположим, что при работе рабочей станции с уровнем мультипрограммирования i поток завершения решений задач является пуассоновским с параметром γ_i, причем γ_i определяется в соответствии с (3).

В этом случае из анализа замкнутой сети с двумя приборами с переменной интенсивностью обслуживания, определяемой выражениями (3) и (5), получаем соотношения для расчета вероятностей P_i (числа заявок в ВК):

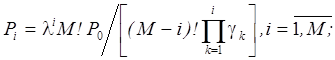                                                                    (6)

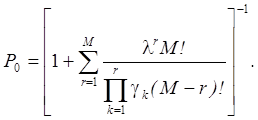
Отсюда среднее время реакции системы выразится как

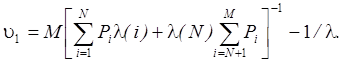                                                                      (7)

Расчеты с использованием (7) показывают, что учет ограничений на уровень мультипрограммирования при применении агрегативного подхода позволяет более точно оценивать основные характеристики функционирования мультипрограммных ВК при конечном числе источников заявок. Особенно это относится к условиям большой загрузки ВК, когда при игнорировании указанных ограничений пропускная способность рабочей станции может быть завышена в несколько раз [1].

В [3] приведена одна из наиболее общих методик реализации агрегативного подхода, основанная на итеративном вычислении характеристик замкнутых сетей МО с общим распределением времени обслуживания заявок в порядке их поступления.

Методика дает точные результаты для сетей, удовлетворяющих условиям локального баланса.

Рассмотрим замкнутую сеть МО, в которой циркулирует I заявок и имеется J узлов обслуживания. Время обслуживания в узле  распределено по некоторому закону B_i(t) со средним b_j1. Заданы вероятности θ_jk перехода в узел k после обслуживания в узле j. Это позволяет рассчитать величины e_j путем решения системы уравнений вида:

.

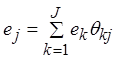Такая сеть именуется сетью А. В соответствии с методикой [3] строится некоторая последовательность сетей A_0, A₁,… аппроксимирующих сеть A. При этом сеть A₀ получается из A путем перехода к экспоненциальному распределению времени обслуживания в узлах с тем же значением среднего времени обслуживания. Сети A_r, r=1,2,… отличаются от A₀ лишь значением среднего времени обслуживания в узлах 1/μ_j(r).

Расчетная процедура методики, определяющая переход от A_k к A_k+1 и условия завершения вычислений, заключается в реализации некоторой последовательности шагов, на первом шаге которой средние значения времени обслуживания в узлах сети A₀ полагаются равными соответствующим величинам в сети A, а распределение времени обслуживания – экспоненциальным. Далее для каждого узла j строится подсистема, содержащая все узлы сети, кроме j. При этом исследуется сеть с двумя узлами, так что выделенная подсистема отображается некоторой СМО, эквивалентной ей в смысле воздействия на узел j (для простоты анализа производится перенумерация: узел j нумеруется как 1, а эквивалентный прибор – как 2).

Для сети с двумя узлами известными методами рассчитываются значения среднего числа заявок в узле j(n_j1) и среднего числа заявок, обслуживаемых в единицу времени (λ_j), а также приведенное среднее число заявок, обслуживаемых в узле j в единицу времени, γ_j=λ_j/e_j. После этого осуществляется проверка сходимости величин n_j1 и γ_j на основе соотношений

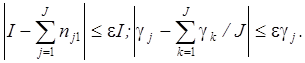                                                                       (8)

Здесь ε – малая величина, задающая порядок допустимой ошибки (например, ε=0,01). Выполнение условий (8) на некоторой итерации указывает на приемлемость полученного отображения A с помощью A₀. В противном случае осуществляется корректировка средних значений времени обслуживания в узлах с помощью выражений (в зависимости от выполнения того или иного из условий (8) и производится следующая (r+1)-я итерация.

Описанная методика использовалась для расчета характеристик некоторых замкнутых сетей, а результаты расчетов сравнивались с результатами имитационного моделирования на ряде экспериментов [3]. В одном из этих экспериментов рассматривалась сеть, в которой число узлов варьировалось от 2 до 5, число заявок – также от 2 до 5, а времена обслуживания полагались распределенными по законам: экспоненциальному, Эрланга 2-го порядка и гиперэкспоненциальному. Результаты эксперимента показали, что расхождение в вычислении значения загрузки узлов не превышает 0,05, а в вычислении среднего числа заявок в узле в основном находится в пределах 0,05. В другом эксперименте исследовались сети из 6-7 узлов, число заявок в которых варьировалось от 2 от 12, а времена обслуживания полагались распределенными по законам гиперэкспоненциальному, Эрланга порядка 2, 4 и 6, экспоненциальному, а также считались постоянными. В результате наблюдалось хорошее согласование вычисляемых характеристик (в пределах 0,05 для загрузки узлов и 0,05J для среднего числа заявок в узле). Расчет тех же сетей точными методами в предположении экспоненциального времени обслуживания давал более значительные расхождения в оценке указанных характеристик.