ОБ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЯХ СУБПОЛОСНЫХ СВОЙСТВ ИЗОБРАЖЕНИЙ
Aннотация
В статье приведены основные вычислительные формулы для определения значений долей энергии в заданных подобластях пространственных частот и сосредоточенности долей энергии. Приведены вычислительные эксперименты по оценке субполосных свойств изображений, которые показывают, что сосредоточенность энергии различных изображений может иметь существенно различающиеся значения.
Ключевые слова: субполосная матрица, подобласть пространственных частот, изображения земной поверхности, доли энергии
Под субполосными свойствами изображений будем понимать характерные особенности в распределении долей энергий изображений в подобластях пространственных частот [1, 2], которые можно использовать для анализа изображений при решении различных задач их обработки, например, при фильтрации, сжатии, внедрении данных и др.
Возможность проведения анализа изображений на основе частотных представлений определяется тем, что в визуальных данных, зачастую, наблюдается периодичность или квазипериодичность отображаемых процессов. На изображении могут присутствовать повторяющиеся объекты, которые задают некоторую периодичность изменения яркости изображения.
В частотной области традиционно обработка изображений предполагает применение преобразования Фурье,
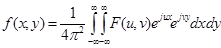 . (1)
. (1)
где f(x,y) – некоторая анализируемая функция. F(u,v) – ее трансформанта Фурье.
Одной из наиболее важных и часто определяемых характеристик на основе преобразования Фурье является часть энергии изображения, попадающей в заданную подобласть пространственных частот (ППЧ),
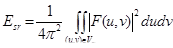 . (2)
. (2)
При описании изображения в виде матрицы  ,
, 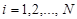 ,
, 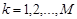 , значения элементов которой определяются значениями яркости пикселей изображения и при специально заданной форме подобласти ПЧ Vsr [3],
, значения элементов которой определяются значениями яркости пикселей изображения и при специально заданной форме подобласти ПЧ Vsr [3],
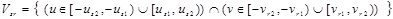 , (3)
, (3)
 ,
, 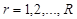 ,
,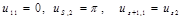 ,
,
 ,
,
выражение (2) может быть преобразовано к виду
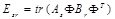 , (4)
, (4)
где Ф – матрица исходного изображения, функция «tr» – след матрицы, As и Br – соответствующие подобласти Vsr субполосные матрицы, размерности NxN и MxM соответственно, элементы которых вычисляются на основании соотношений, приведенных в [4].
В процессе анализа изображений целесообразно использовать значения долей Psr энергии изображения [5], соответствую-щих заданной подобласти ПЧ Vsr,
 .
.
В работе [6] для случая разбиения области ПЧ (2) на равновеликие подобласти вида (3) введено понятие частотной сосредоточенности Cm для доли m энергии изображения как отношение минимального количества lm подобластей ПЧ, в которых сосредоточено m·100 процентов энергии изображения, к общему числу подобластей ПЧ,
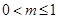 , (5)
, (5)
 . (6)
. (6)
Алгоритм определения указанного минимального количества lm подобластей ПЧ приведен в [6].
Обозначим, Mm – множество подобластей ПЧ, соответствующих указанному количеству lm. Подобласти ПЧ, входящие в множество Mm, в работе [7] названы информационными подобластями пространственных частот.
Применение указанных понятий позволяет построить процедуры анализа субполосных свойств изображений земной поверхности, под которыми будем понимать характерные особенности в распределении долей энергий изображений в подобластях ПЧ, которые можно использовать при решении различных задач обработки изображений, например, при внедрении данных.
Размерность анализируемых изоб-ражений выбрана равной 256×256 пикселей, разбиение области ПЧ было осуществлено на 64×64 подобласти ПЧ. Выбор указанных параметров не снижает общности полученных результатов.
Анализ разбиения осуществлен на основании значений элементов матрицы долей энергий изображений в соответствующих подобластях ПЧ, а также на основании графиков, отображающих значения элементов матрицы долей энергий, которые расположены на различных строках, столбцах и диагоналях данной матрицы.

Рис. 1. Исходное изображение (И1)
Fig. 1. The original image (I1)
Экспериментальные исследования распределения значений долей энергии изображения, приведенного на рисунке 1, выполнены с целью демонстрации наличия подобластей ПЧ, соответствующих относительно большим значениям долей энергии изображений, и подобластей ПЧ, которым соответствуют доли энергии значительно меньшие по значению, и которыми при решении различных задач обработки изображений можно пренебречь. Анализируемые изображения были выбраны так, чтобы соответствующие частотные сосредоточенности (6) энергии имели существенно различные значения.
Для изображения И1 (рисунок 1) отдельные фрагменты матрицы P=(Psr), s=1,2,...,64, r=1,2,...,64, содержащей значения долей энергии, вычисленные при разбиении области ПЧ на 64×64 равновеликих подобласти, приведены в таблицах 1-3.
Таблица 1
Доли Psr энергии изображения И1 в ППЧ Vsr (S=R=64, s=1,2,...,12, r=1,2,...,8)
Table 1
The shares Psr of image energy I1 in SSF Vsr (S=R=64, s=1,2,...,12, r=1,2,...,8)
r s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
1 | 5,84E-01 | 1,40E-01 | 2,69E-02 | 1,48E-02 | 8,60E-03 | 4,01E-03 | 2,08E-03 | 1,63E-03 |
2 | 4,36E-02 | 3,57E-02 | 6,23E-03 | 3,95E-03 | 2,17E-03 | 3,94E-04 | 5,09E-04 | 4,60E-04 |
3 | 1,29E-02 | 4,74E-03 | 1,94E-03 | 2,67E-03 | 1,26E-03 | 6,40E-04 | 5,53E-04 | 4,81E-04 |
4 | 5,00E-03 | 2,61E-03 | 2,61E-03 | 3,04E-03 | 1,14E-03 | 4,66E-04 | 7,64E-04 | 6,05E-04 |
5 | 3,51E-03 | 1,51E-03 | 2,13E-03 | 5,30E-04 | 3,96E-04 | 2,48E-04 | 4,78E-04 | 3,59E-04 |
6 | 2,88E-03 | 1,48E-03 | 1,13E-03 | 8,75E-04 | 1,73E-04 | 1,35E-04 | 6,13E-04 | 2,82E-04 |
7 | 1,53E-03 | 3,41E-04 | 2,98E-04 | 6,46E-04 | 5,43E-04 | 3,43E-04 | 4,69E-04 | 3,34E-04 |
8 | 9,73E-04 | 4,39E-04 | 2,87E-04 | 2,75E-04 | 2,66E-04 | 3,23E-04 | 2,60E-04 | 4,63E-04 |
9 | 6,75E-04 | 2,47E-04 | 1,60E-04 | 3,69E-04 | 1,46E-04 | 1,98E-04 | 1,37E-04 | 2,09E-04 |
10 | 7,63E-04 | 3,46E-04 | 3,39E-04 | 2,05E-04 | 2,07E-04 | 2,00E-04 | 1,73E-04 | 1,40E-04 |
11 | 5,88E-04 | 2,17E-04 | 1,92E-04 | 8,07E-05 | 1,82E-04 | 9,04E-05 | 8,05E-05 | 1,35E-04 |
12 | 3,91E-04 | 1,09E-04 | 9,53E-05 | 1,33E-04 | 8,20E-05 | 1,01E-04 | 1,36E-04 | 1,33E-04 |
Таблица 2
Доли Psr энергии изображения И1 в ППЧ Vsr (S=R=64, s=26,27,...,37, r=26,27,...,33)
Table 2
The shares Psr of image energy I1 in SSF Vsr (S=R=64, s=26,27,...,37, r=26,27,...,33)
r s | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
26 | 4,44E-06 | 5,35E-06 | 5,06E-06 | 9,61E-06 | 6,64E-06 | 1,89E-06 | 2,36E-06 | 2,32E-06 |
27 | 5,93E-06 | 4,87E-06 | 1,20E-05 | 4,27E-06 | 3,73E-06 | 7,03E-06 | 1,69E-06 | 1,69E-06 |
28 | 6,15E-06 | 4,59E-06 | 5,64E-06 | 3,14E-06 | 5,61E-06 | 3,67E-06 | 1,84E-06 | 2,92E-06 |
29 | 6,03E-06 | 3,04E-06 | 4,97E-06 | 1,04E-05 | 5,34E-06 | 4,49E-06 | 1,49E-06 | 2,24E-06 |
30 | 4,53E-06 | 6,78E-06 | 1,13E-06 | 4,64E-06 | 5,51E-06 | 2,62E-06 | 1,46E-06 | 1,84E-06 |
31 | 5,85E-06 | 2,78E-06 | 4,24E-06 | 3,07E-06 | 2,06E-06 | 3,28E-06 | 4,17E-06 | 1,27E-06 |
32 | 8,18E-06 | 3,72E-06 | 4,11E-06 | 2,78E-06 | 2,10E-06 | 2,23E-06 | 1,30E-06 | 1,30E-06 |
33 | 4,36E-06 | 5,28E-06 | 2,36E-06 | 1,87E-06 | 1,92E-06 | 2,70E-06 | 2,51E-06 | 3,22E-06 |
34 | 3,12E-06 | 5,77E-06 | 2,79E-06 | 3,22E-06 | 2,40E-06 | 4,32E-06 | 3,91E-06 | 2,11E-06 |
35 | 3,91E-06 | 6,20E-06 | 6,85E-06 | 3,95E-06 | 4,23E-06 | 3,06E-06 | 3,80E-06 | 2,86E-06 |
36 | 6,16E-06 | 4,19E-06 | 2,90E-06 | 3,44E-06 | 1,99E-06 | 1,60E-06 | 2,93E-06 | 2,35E-06 |
37 | 3,07E-06 | 2,36E-06 | 3,93E-06 | 4,58E-06 | 3,19E-06 | 2,89E-06 | 1,85E-06 | 1,65E-06 |
Таблица 3
Доли Psr энергии изображения И1 в ППЧ Vsr (S=R=64, s=53,54,...,64, r=57,58,...,64)
Table 3
TThe shares Psr of image energy I1 in SSF Vsr (S=R=64, s=53,54,...,64, r=57,58,...,64)
r s | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 |
53 | 1,28E-07 | 1,91E-07 | 1,96E-07 | 1,50E-07 | 1,13E-07 | 1,62E-07 | 1,28E-07 | 1,41E-07 |
54 | 2,67E-07 | 1,73E-07 | 1,66E-07 | 1,80E-07 | 1,65E-07 | 1,19E-07 | 7,73E-08 | 1,22E-07 |
55 | 1,22E-07 | 1,06E-07 | 2,48E-07 | 2,04E-07 | 2,20E-07 | 1,17E-07 | 1,58E-07 | 2,37E-07 |
56 | 1,92E-07 | 1,62E-07 | 1,62E-07 | 1,34E-07 | 1,48E-07 | 1,19E-07 | 1,57E-07 | 1,65E-07 |
57 | 2,03E-07 | 1,40E-07 | 8,89E-08 | 1,52E-07 | 8,63E-08 | 1,11E-07 | 1,26E-07 | 1,18E-07 |
58 | 1,35E-07 | 9,95E-08 | 9,93E-08 | 1,01E-07 | 1,05E-07 | 1,16E-07 | 1,00E-07 | 1,54E-07 |
59 | 1,19E-07 | 1,20E-07 | 8,09E-08 | 1,08E-07 | 1,38E-07 | 1,35E-07 | 1,27E-07 | 1,40E-07 |
60 | 1,95E-07 | 1,32E-07 | 1,21E-07 | 1,09E-07 | 1,24E-07 | 6,86E-08 | 1,22E-07 | 9,38E-08 |
61 | 1,31E-07 | 1,37E-07 | 1,29E-07 | 1,04E-07 | 5,42E-08 | 2,00E-07 | 2,06E-07 | 1,96E-07 |
62 | 1,18E-07 | 1,28E-07 | 8,91E-08 | 1,14E-07 | 1,26E-07 | 1,13E-07 | 8,60E-08 | 1,43E-07 |
63 | 1,63E-07 | 1,24E-07 | 8,80E-08 | 9,55E-08 | 1,21E-07 | 8,12E-08 | 1,13E-07 | 9,73E-08 |
64 | 2,16E-07 | 1,18E-07 | 1,10E-07 | 1,53E-07 | 1,73E-07 | 9,30E-08 | 1,24E-07 | 5,80E-08 |
Данные, приведенные в таблицах 1-3, показывают, что подобластям Vik, i=1,2,...,9, k=1,2,...,7 (таблица 1) соответствуют значительные доли энергии изображения И1 (рисунок 1). При этом в подобластях Vik, i,k=26,27,28,29, (таблица 2) сохраняются относительно большие значения долей энергии, что указывает на наличие на изображении характерных периодически повторяющихся линий; подобластям Vik, i=53,54,...,64, k=57,58,...,64, (таблица 3) соответствуют доли энергии значительно меньшие по значению, чем в подобластях, приведенных в таблице 1, что позволяет пренебречь данными значениями при осуществлении различных операций по обработке изображений, например, фильтрации и внедрении данных.
Для более наглядного анализа распределения значений долей энергии изображения И1 (рисунок 1) можно использовать приведенные на рисунке 2 в виде диаграмм значения, соответствующие различным строкам, столбцам и диагоналям матрицы P=(Psr), s=1,2,...,64, r=1,2,...,64, долей энергии.
На диаграммах, приведенных на рисунке 2, наглядно видно наличие подобластей ПЧ, соответствующих несущественным значениям долей энергии.
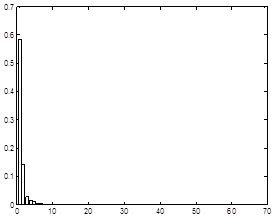
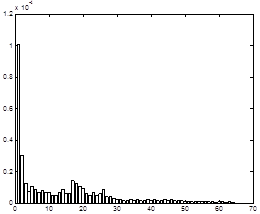
Первая строка Средняя строка

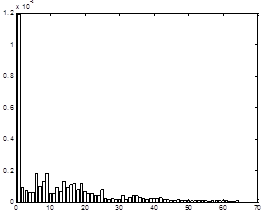
Первый столбец Средний столбец


Главная диагональ Побочная диагональ
Рис. 2. Доли энергии изображения И1, соответствующие отдельным элементам матрицы долей энергии
Fig. 2. Shares of image energy I1 corresponding to the individual elements of the energy shares of matrix
Аналогичные результаты анализа распределения значений долей энергии получены и для других изображений, что указывает на возможность применения долей энергии для анализа изображений.
Следующие результаты вычислительных экспериментов показывают возможность применения для анализа изображений значений долей энергии, полученных при разбиении области ПЧ на различное количество подобластей. Различные разбиения области ПЧ на подобласти позволяют выполнить анализ изображений с различной степенью детализации их частотных свойств.
На рисунке 3 приведены диаграммы значений долей энергии изображения И1, приведенного на рисунке 1, при разбиении области ПЧ на 64×64, 32×32, 16×16 и 8×8 равновеликих ППЧ. Для повышения наглядности значение доли энергии в подобласти V11 (значительно превышающее другие значения) на диаграммах не отображено.


64×64 32×32
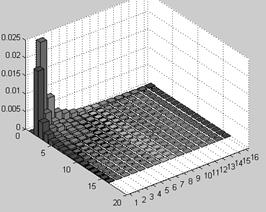

16×16 8×8
Рис. 3. Распределение долей энергии изображения И1 при различных разбиениях области ПЧ
Fig. 3. The distribution of the image I1 energy shares in different decompositions of the SF field
Данные, приведенные на рисунке 3, наглядно показывают наличие относительно больших и малых значений долей энергии в различных ППЧ и позволяют с различной степенью детализации анализировать их распределение в области ПЧ.
Аналогичные результаты были получены и для других изображений.
Следующие экспериментальные иссле-дования проведены с целью определения значений сосредоточенности (6) энергии изображений при различных значениях доли m энергии в зависимости от количества S подобластей ПЧ.
Для изображения И1 (рисунок 1) сосредоточенность определена при значениях доли m=0,94¸0,99 энергии изображения при разбиении области ПЧ на 64×64 равновеликих подобласти. На рисунке 4 информационные подобласти ПЧ, опре-деляющие значение сосредоточенности и соответствующие заданным значениям доли m энергии изображения, отображены серым цветом.
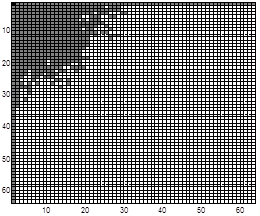

m=0.99 m=0.98

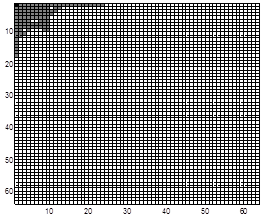
m=0.97 m=0.96


m=0.95 m=0.94
Рис. 4. Информационные подобласти ПЧ, соответствующие заданным значениям доли m энергии изображения И1
Fig. 4. Information subdomains of SF corresponding to given values of the share m of image I1 energy
Изображения подобластей, приведенные на рисунке 4, показывают, что можно указать такие изображения земной поверхности для которых информационными являются подавляющее большинство подобластей ПЧ, что необходимо учитывать, например, при решении задач фильтрации и внедрения данных.
В таблице 4 приведены соответствующие рисунку 4 значения сосредоточенности C энергии изображения И1 и соответствующее количество N1 информационных подобластей ПЧ для различных значенийm и при различном разбиении области ПЧ на SxR подобластей.
Таблица 4
Сосредоточенность энергии изображения И1 и количество информационных подобластей ПЧ
Table 4
Energy concentration of image I1 and the amount of information subdomains of SF
S=R m | 8 | 16 | 32 | 64 | ||||
C | N1 | C | N1 | C | N1 | C | N1 | |
0,99 | 0,188 | 12 | 0,172 | 44 | 0,156 | 160 | 0,143 | 586 |
0,98 | 0,094 | 6 | 0,086 | 22 | 0,079 | 81 | 0,072 | 296 |
0,97 | 0,063 | 4 | 0,047 | 12 | 0,045 | 46 | 0,042 | 172 |
0,96 | 0,047 | 3 | 0,031 | 8 | 0,028 | 29 | 0,026 | 105 |
0,95 | 0,031 | 2 | 0,020 | 5 | 0,019 | 19 | 0,017 | 70 |
0,94 | 0,016 | 1 | 0,016 | 4 | 0,013 | 13 | 0,012 | 48 |
Из таблицы 4 видно, что на значение сосредоточенности энергии изображения практически не оказывает влияние увеличение числа S подобластей ПЧ, на которые разбивается область ПЧ. Эксперименты также показали, что для изображения И1 при уменьшении величины доли m энергии изображения соответствующие значения сосредоточенности и количество информационных подобластей уменьшаются незначительно, что не позволяет иметь широкий выбор ППЧ, например, для внедрения данных.
На основании данных, приведенных в таблице 4, построены отображенные на рисунках 5 графики значений сосредоточенности энергии изображения в зависимости от доли m энергии указанных изображений при различных значениях количества S подобластей ПЧ.

Рис. 5. Сосредоточенность энергии изображения И1
Fig. 5. Energy concentration of image I1
Данные, приведенные в таблице 4, а также на рисунке 5, показывают, что сосредоточенность энергии не превышает 0,19 для изображения И1 при значении доли энергии m=0.99.
В ходе проведения вычислительных экспериментов были выполнены аналогичные эксперименты с различными изображениями земной поверхности. Следует отметить, что подобные распределения значений сосредоточенности энергии характерны для большинства исследованных изображений.
Результаты экспериментов показали, что сосредоточенность энергии различных изображений может иметь существенно различающиеся значения, что, например, может влиять на объем внедряемых в изображения данных. Полученные результаты вычислительных экспериментов могут служить основой (рекомендациями) для выделения информационных компонент изображений, например, при решении задач фильтрации и внедрения данных.
Проведенный анализ распределения долей энергий изображений в подобластях ПЧ также показал, что имеются отдельные подобласти ПЧ, в которых практически отсутствует энергия изображений, что может быть использовано в задачах обработки изображений.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 15-07-01570.
















Список литературы
1. Гонсалес, Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс. – М.: Техносфера, 2006. – 1072 с.
2. Сойфер, В. А. Методы компьютерной обработки изображений / В. А. Сойфер. – М.: ФИЗМАТЛИТ, 2003. – 784 с.
3. Жиляков, Е.Г., Черноморец А.А. О частотном анализе изображений // Вопросы радиоэлектроники. Сер. ЭВТ. – 2010. – Вып. 1. – С. 94-103.
4. Жиляков, Е.Г., Черноморец А.А., Заливин А.Н. Об эффективности метода оценивания значений долей энергии изображений на основе частотных представлений // Известия ОрелГТУ. Информационные системы и технологии. – № 2/52 (563) март-апрель. – 2009. – С. 12-22.
5. Черноморец А.А., Иванов О.Н. Метод анализа распределения энергий изображений по заданным частотным интервалам // Научные ведомости Белгородского государственного университета. Серия: Экономика. Информатика. 2010. Т. 19. № 16-1. С. 161-166.
6. Черноморец, А.А. Голощапова В.А., Лысенко И.В., Болгова Е.В. О частотной концентрации энергии изображений // Научные ведомости БелГУ. Сер. История. Политология. Экономика. Информатика. – 2011. – № 1(96). – Вып. 17/1. – С. 146-151.
7. Жиляков Е.Г., Черноморец А.А., Голощапова В.А. Реализация алгоритма внедрения изображений на основе использования неинформационных частотных интервалов изображения-контейнера // Вопросы радиоэлектроники. 2011. Т. 4. № 1. С. 96-104.