Оценивание качества работы контуров регулирования технологического процесса (ТП) травления холоднокатаной стали в непрерывном травильном агрегате (НТА) является нетривиальной задачей. Процедура основана на оценивании средних значений остатков нормированной величины 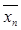 (доли площади остаточных дефектов) и их отклонений [2]. Средние значения каждой суммарной статистики обновляются по следующему правилу:

,                (1)

где 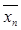 – рассчитанное по n точкам среднее значение остатка; x_n – данные для новой точки;  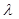– фильтрующий коэффициент.

Рассчитанные относительные изменения средних значений остатков и их отклонений могут быть использованы в качестве входных сигналов нейронной сети для классификации локального дефекта качества (Q_n) и при формировании управляющих воздействий в ТП. Этот коэффициент предлагается вычислять следующим образом:

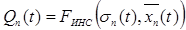,                     (2)

где F_ИНС – нейросетевая модель; 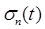 и 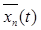 – соответственно среднеквадратичное отклонение и среднее значение остатка в рабочем окне n (рассчитанное по n точкам в момент времени t). Оценка средних значений нормированных по площади остатков дефектов поверхности полосы и их отклонений предложена как критерий оперативного контроля качества ТП.

В [1] была формализована задача травления и предложен нечеткий классификатор дефектов (Д): систематических по краям рулона стальной полосы и несистемных (НД) в виде окалины различных толщин d_n и оттенков серого цвета. Идентификацию цвета Д предложено осуществлять по яркостной компоненте, формула перехода к которой представлена в [12]:

Y=R*0.299+G*0.587+B*0.114,                  (3)

где Y – яркость в оттенках серого цвета; R,G,B – цветовые составляющие в диапазоне 0¸255.

Скорость травления стальной полосы – t_Р в сернокислотных травильных растворах (ТР) нелинейно связана уравнением Аррениуса [3] со следующими управляемыми параметрами ТП: Т – температурой раствора, С – концентрацией травильного раствора (КТР) серной кислоты, Сn – концентрацией мультигидратов сульфата железа в ТР. ТП травления полосовой стали как типичная конвейерная линия [9], может быть формализован нечеткой MISO – моделью вида Х → Y.

Гиперповерхность модели t_Р=f(Т,С,Сn), для которой из аналитических зависимостей известны значения (Х;Y), строится по m опорным точкам измерений параметров, принятых в качестве центров-медиан классов. Фрагменты гиперповерхности представлены на рисунке 1. Аналогично процедуре, приведенной в [11] для построения нейронной RBF-сети в каждом из m классов определена GRB-функция активации:

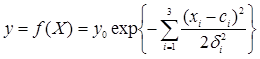.         (4)

На выборке экспериментальных данных с учетом рекомендаций, приведенных в [10], были проведены настройка центров c_i и величин охвата ветвей 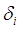 путем последовательного «обучения сети с учителем» [7].

Построенная RBF-сеть дефаззифицирует входные параметры методом одноточечных множеств, определяя оптимальные стратегии ТП травления металла при регламентных ограничениях по срезу (Т, С), и поддерживает скорость травления на заданном уровне.

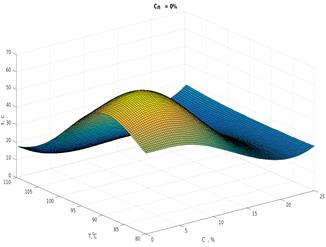
а) 80ºС < Т, С < 25%, Сn=0%                                                б) 80ºС < Т, С < 25%, Сn=15%

Рис. 1. Гиперповерхность модели t_Р = f (Т, С, Сn)

Fig. 1. The model’s hypersurface t_Р= f (Т, С, Сn)

Для достижения качественного травления, температуры растворов должны постоянно поддерживаться на таком уровне, чтобы показатель времени травления t_Р был максимален в каждой травильной ванне. Определение оптимальных температур ТР зависит от сортамента и качества полосы проката, условий ведения процесса, и скорости потери активности ТР.

Оптимальная стратегия ТП травления холоднокатаной стали заключается в том, что постепенное снижение КТР компенсируется повышением температуры в ваннах до максимального предела, определенного регламентом (от 88 °С до 99 °С). Управление параметрами осуществляется по критерию, применяемому к (4):

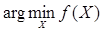.                       (5)

Критерий приведен к стоимостной шкале в упрощенной аддитивной форме введением скаляра нормированных коэффициентов удельных затрат E на изменение каждого из управляемых параметров ∆Х, и имеет вид:

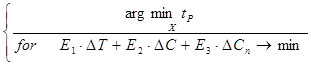.                (6)

Определение значений E, с учетом взаимного влияния элементов Х на ход ТП, проводилось в виде экспертной процедуры, предложенной в [8].

Скорость реакции травления – t_Р зависит от: стартовой энергии активации травильного раствора – E_a, прямо пропорциональна корню касательного напряжения потока травильного раствора – 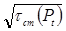, создаваемого на поверхности дефекта давлением потока P_t с расстояния от сопла до поверхности l [1]:

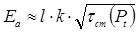.                       (7)

Этот эффект использован для гидравлического смыва дефектов [4] в 1-ой ванне НТА, с предварительной идентификацией их характеристик: координат и цветовой RGB-оценки, которая нечетко определяет величину давления, с которой подается ТР на дефектную область полосы. Управление давлением ТР, подаваемого из сопла, производится по закону вида Р_t=f (d_n).

В отличие от зарубежных аналогов, описанных в [1], где накапливалась статистика НД на выборке из партии рулонов стальной полосы, и отсутствовал выходной контроль Im^out, в [4] была предложена схема НТА с компараторной идентификацией дефектов, представленная на рисунке 2.

Устройство содержит: 1 – травильный агрегат с узлами нагрева, рекуперации и регенерации травильного раствора; 2 – металлическую полосу; 3 – блок регулирования давления Р_t травильного раствора в соплах устройства гидравлического орошения несистемных дефектов, расположенных по N единиц по обеим сторонам плоскости движущейся металлической полосы; 4 – оптический датчик выходного контроля качества травления металлической полосы с обеих сторон; 5 – блок обработки оптической информации и управления технологическим процессом; 6 – дозатор; 7 – оптический датчик входной идентификации и позиционирования несистемных дефектов металлической полосы с обеих сторон; 8 – ванна орошения травильного агрегата; 9 – второй дозатор; 10 – комплекс погружных травильных ванн (или одну травильную ванну).

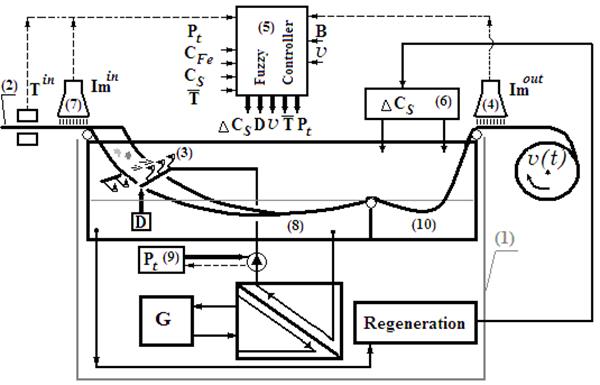
Рис. 2. Схема НТА с идентификацией и позиционированием несистемных дефектов полосы проката

Fig. 2. Scheme of CPA with the identification and positioning of rolled strip’s non-system defects

Процесс обработки поверхности полосы происходит следующим образом. Получая данные от (7) контроллер (5) определяет позиционные координаты m–го дефекта D^m в виде прямоугольника с координатами диагональных вершин (х₁^m , y₁^m) и (х₂^m , y₂^m), и формирует сигнал на (3) для включения сопел N_j (j=i,i+1,…,k) на период времени Т_j=(y₂^m–y₁^m)/v(t). Причем область орошения сопел N_j покрывает дефект D^m на участке полосы шириной [х₁^m , х₂^m]. Контроллер (5) формирует сигнал (9) для изменения номинала площади проходного сечения А_j сопла, с целью достижения на выходе сопла N_j давления травильного раствора Р_t в соответствии со значением функции возможности π_n(X_m= «Цвет»). Интерпретируемое управляющее воздействие – изменение сечения сопла (давления) подачи травильного раствора Р_i в i-м сопле орошения, позиционно покрывающим область координат дефекта (с уточнением ΔР_t в процессе обучения синтезируемого нечеткого регулятора). Логическое правило управления (ЛПУ) селективным травлением полосы формируется следующим образом:

ЕСЛИ (Цвет= Х_m & D^m) ТО ((включить N_j сопла, j=i, i+1,…,k) & (изменить площади сечений А_j, j= i, i+1,…,k в соответствии π_n(Х_m)).            (8)

Дефаззифицируя ЛПУ, получим:

ЕСЛИ (Х_m(t_i) & D^m (t_i)) ТО [А_j (t_i`)=А_j (π(Х_m(t_i))) & А_j (t_i+Т_j)=А_j (π(Х_m(t_i+Т_j))],            (9)

где t_i`=t_i–τ_on+(L_7–3/V(t)), для j=i,…,k – момент реального времени включения сопла; L_7–3 – длина участка проката с учетом петли от точки входной идентификации (датчика 7), которую точка до сопел (3) преодолевает за время t_7–3 со скоростью сматывания полосы V(t) (максимум 120 м/с); τ_on – время задержки системы управления для изменения площади проходных сечений А_j; Т_j – период времени включения сопла для обработки дефекта D^m(Х_m(t_i)).

Отсутствие априорной информации об НД (количестве, форме, размерах) приводит к методике применения нечеткой кластеризации входных данных Imⁱⁿ. Для минимизации ошибки неразличимости НД, находящихся в геометрической близости друг от друга [5] при влиянии фоновых ошибок телеметрической аппаратуры, предложен метод входной сегментации НД.

По наборам позиционных координат части НД относят к разным сегментам S_i полосы проката. Ширина сегмента S_j соответствует по размеру орошаемой части полосы поверхности проката соплом А_j в момент отработки управляющего воздействия. ЛПУ давлением Р_t для сопла А_j с учетом (8) можно представить в виде:

А_j (t_i`): Р<sub>j</sub> (t<sub>i</sub>`) (R {Х_m(t_i) | D^m (t_i) ϵS_j}),            (10)

где R – определяющее правило преобладающей альтернативы. Физически обусловленные ограничения на количество сопел N приводят к неоднозначностям управляющих воздействий для обработки НД. В секторе S_j обработки поверхности соплом А_j могут одновременно находиться дефекты с различными цветовыми характеристиками Х_m. Отношение R, определяющее предпочтительную ветвь алгоритма управления, задает правило воздействия на сектор: минимальное, усредненное или максимальное изменения давления в сопле или КТР, и устраняет нечеткость управления. Рисунок 3 иллюстрирует правило R: max (Р_t) для сопла А2 на временном отрезке (t₁;t₄). При дефаззификации ЛПУ функция π(Х_m(t_i)) заменяется числовой оценкой цвета дефекта по формуле (3).

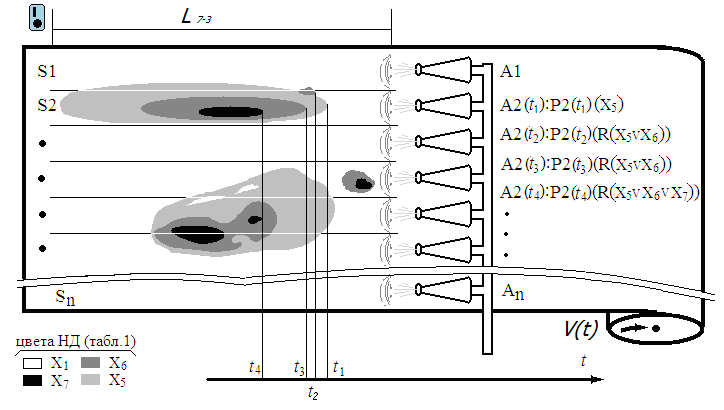
Рис. 3. Входная сегментация несистемных дефектов полосы проката

Fig. 3. The input segmentation of rolled strip’s non–system defects

Экспертами электротехнической и химической лабораторий завода экспериментально был составлен классификатор с параметрами управляющих воздействий, приводящих к полному удалению НД при предварительном входном гидравлическом воздействии с давлением подачи ТР на сопла Р_t=(0; 6) МПа и последующем прохождении ими всех ванн НТА.

В качестве исполнительного устройства применялся титановый клапан типа Н331g диаметром сечения 5мм с равномерной линеаризованной характеристикой, оснащенный редукторным электрическим приводом ANT 5 производства фирмы AS Shneider.

Время полного хода шпинделя от закрытого состояния клапана до открытого составляет t_f=5с. Значения времени хода шпинделя от закрытого состояния клапана до открытых состояний с достижением соответствующих значений Р_t приведены в таблице 1. На примыкающих отрезках зависимости t_f(i,i+1)=F(Р_t(i,i+1)) проявляются линейно для i=1,…,n.

Таблица 1

Классификатор НД и параметры управляющих воздействий

Table 1

Qualifier of non-system defects and control actions parameters

Характеристика зависимости давления от времени хода шпинделя ΔР_t (Δ t_f) линеаризована на участках (Р_t(i);t_f(i))–(Р_t(i+1);t_f(i+1)) за счет сложной геометрии камеры игольчатого клапана. Направление отработки движения А(ΔY) шпинделя клапана определяется знаком отклонения оценки Y(D_m(t_i+1)), полученной в момент t_i+1:

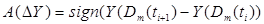.      (11)

Величина хода иглы клапана зависит от длительности времени включения электропривода, приводящего в движение шпиндель.

Решение основано на FCM-методе кластеризации [10] характеристики Р_t (Па) от яркостной оценки цвета дефекта – Y. Область определения Y=[0; 231] разделяется на n неравных подобластей-кластеров с центрами-медианами назначаемыми в опорных точках с известными характеристиками (Y_n, Р_{t n}).

Интерполяция Р_t(Y) внутри класса осуществляется с помощью GRB-функций аналогично (4). При этом Y_i и Y_i–1 принимаются как центры соседних кластеров. Текущее значение оценки Y(t)=y_j относят к i-му классу по критерию минимума Евклидова расстояния от оцениваемого объекта до центра i-го кластера Y_i. Для каждого i-го кластера (i=1,2,3,…,7) строятся несимметричные функции принадлежности типа:

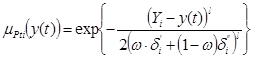,        (12)

где l – настраиваемый степенной показатель, влияющий на сглаживание функции, принят равным 4; δ – настраиваемая величина отклонения функции принадлежности к кластеру, к реализации принята равной 0,3 минимального расстояния до центра ближайшего кластера; ω – логическая переменная  типа:

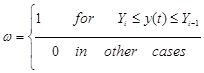            (13)

Для i=1 область определения y(t)≤231, поэтому для i=2 функция принадлежности принимает вид в соответствии с параметрами из таблицы 1:

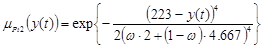,     (14)

где ω=1 для 223<y(t)≤229 и ω=0 для других значений y(t). Аналогично строится функция для i=7.

На рисунке 4 представлен график t_f(Р_t). Предложенное решение позволяет нечетко вычислять необходимые значения Р_t(y(t)) в каждый момент времени для сопла А_j. Время задержки системы управления для изменения площади проходного сечения сопла τ_on определяется по линейному закону, адаптивно изменяющемуся на разных отрезках ∆Р_t.

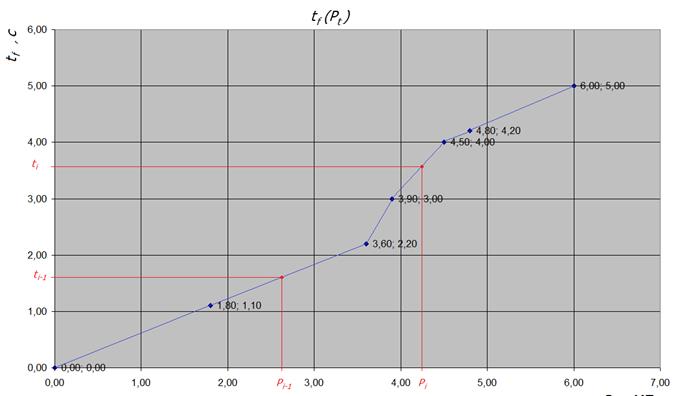
Рис. 4. Скорость изменения площади проходного сечения сопла t_f(Р_t)

Fig. 4. The change rate of flow section of the nozzle square t_f(Р_t)

Непрерывная функция t_f(Р_t) кусочно линеаризуется на области определения Р_t=(0; 6) c разбиением на n неравных классов, границы которых обозначены соседними синими точками на рисунке 4, с условно постоянными законами t_f(Р_t) внутри подобластей. С целью изменения давления на величину ΔР_t , время включения электропривода Δt_f изменяется по пропорциональному закону с коэффициентом k_n внутри n-го класса:

.                                (15)

Принадлежность величины Р_t(t_i) n-му классу определяется неравенством 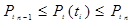 и, при известном линейном законе t_f(Р_t), внутри классов, t_f i определяется по адаптивному закону управления:

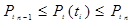:                        (16)

При известном значении предыдущей итерации t_f(i-1) время задержки по управлению определяется как:

τ_on=‖t_f(i)–t_f(i–1)‖,                    (17)

а момент реального времени включения сопла:

t_i`=t_i–τ_on+(L_7–3/V(t)).               (18)

Длительность периода времени включения определена как Т_j=(y₂^m–y₁^m)/v(t), направление вращения определяется по формуле (11).