ПРИМЕНЕНИЕ ПРОГРАММНОГО КОМПЛЕКСА «UFOMODELER» ДЛЯ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА С ИСПОЛЬЗОВАНИЕМ НЕКОТОРЫХ ЧИСЛЕННЫХ МЕТОДОВ
Aннотация
В работе рассматривается процесс итеративного вычисления дифференциального уравнения первого порядка в виде последовательных этапов с применением программного комплекса «UFOModeler».
Ключевые слова: системно-объектный подход «Узел-Функция-Объект», визуальное графоаналитическое моделирование, обыкновенные дифференциальные уравнения, численные методы
Введение
Задачи имитационного моделирования функционирующих систем очень часто сводятся к необходимости формального описания протекающего процесса, модель которого необходимо построить. В свою очередь множество процессов можно описать определенным дифференциальным уравнением.
Исходя из вышесказанного, для моделирования численных алгоритмов решения дифференциальных уравнений будет выбран системный подход «Узел-Функция-Объект» как единый универсальный подход к исследованию явлений любой природы [1, с. 2]. Данный подход, в том числе, призван обеспечить возможность универсального представления всех видов знаний.
Упомянутый подход является относительно новым и может быть использован для моделирования численных алгоритмов решения дифференциальных уравнений. До настоящего времени данный подход использовался как средство моделирования бизнес-процессов, организационных знаний, а также слабо формализуемых предметных областей. Использование предлагаемого подхода для представления знаний с целью моделирования процесса решения дифференциальных уравнений обусловлено следующими соображениями.
Предметная область, в рамках которой осуществляется вычислительный процесс, сама представляет собой сложную систему. Следовательно, знания об этой предметной области также должны представлять собой систему. Анализ, рассмотренных в литературе по вычислительной математике и численным методам, видов представления дифференциальных уравнений показал, что все виды дифференциальных уравнений могут быть сведены к трем базовым видам: данным о зависимых и независимых параметрах функций (на уровне входов-выходов), процедурным данным (о динамике ее функционирования) и декларативным данным о субстанции системы (об объекте, выполняющем функцию). Представленные соображения и обуславливают использование УФО-подхода для решения задач данного исследования.
Основная часть
На текущем этапе исследования целью являлось моделирование процесса решения обыкновенных дифференциальных уравнений с использованием численных методов анализа в терминах формализованного графоаналитического подхода «Узел-Функция-Объект».
Для достижения цели необходимо выполнить следующие задачи:
- адаптировать УФО-подход к задаче представления математических данных с целью моделирования процесса решения обыкновенных дифференциальных уравнений;
- разработать диаграммы, отражающие процесс решения обыкновенных дифференциальных уравнений первого порядка в терминах «Узел-Функция-Объект»;
- представить результаты вычислений;
- построить графики функций с помощью программы UFOModeler;
- сделать вывод о точности математических вычислений программного обеспечения UFOModeler.
Будем рассматривать процесс итеративного вычисления дифференциального уравнения первого порядка в виде последовательных этапов, каждый из которых обладает результатом. Причем любая связь (поток) вычислительного процесса представляет собой набор качественных и количественных показателей некоторого объекта, который создается или выполняется в рамках текущего вычислительного процесса.
Рассмотрим пример решения обыкновенного дифференциального уравнения первого порядка с помощью метода Эйлера-Коши:
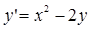 (1)
(1)
Метод Эйлера-Коши является модификацией метода Эйлера и имеет второй порядок точности вычисления.
Контекстная модель такого процесса представлена на рисунке 1.
Исходя из рисунка 1, процесс вычисления дифференциального уравнения (1) можно рассматривать как определение функции y от «независимых параметров», к ним относят: интервал на котором рассматривается функция [0..1], шаг разбиения интервала – 0.1.
При этом зададим начальное условие решения y(0)=1 – «зависимый параметр».
Первый узел диаграммы «инкремент шага h» отвечает за проход по всему интервалу вычисления функции с заданным в условии шагом. Данный узел образует связь с узлом «вычисление приращения Dy», в котором выполняется вычисление 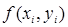 и
и 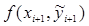 :
:
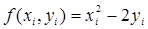 , (2)
, (2)
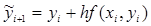 , (3)
, (3)
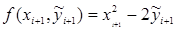 , (4)
, (4)
где i=0,1,2,...,n.
Число n – количество шагов, определяемое как отношение интервала к размеру шагу:
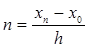 (5)
(5)
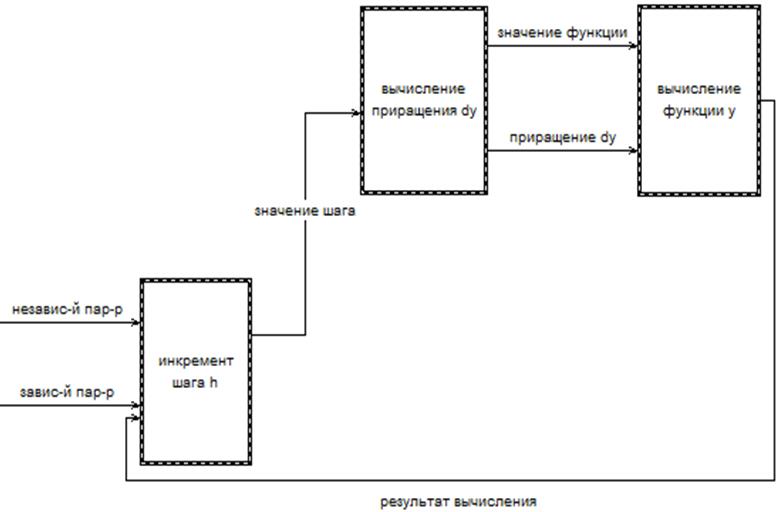
Рис. 1. Контекстная модель процесса вычисления дифференциального уравнения первого порядка
Fig. 1. The contextual process model calculations differential equation
Геометрически это означает, что сначала определяется направление интегральной кривой в исходной точке (xi, yi) и во вспомогательной точке 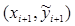 , а в качестве окончательного направ-ления берется ср1еднее значение этих направ-лений.
, а в качестве окончательного направ-ления берется ср1еднее значение этих направ-лений.
Далее параметры, которые были определены в текущем узле, передаются к следующему связанному узлу «вычисление функции y» в котором определяется значение функции на текущем шаге интервала:
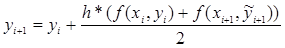 , (6)
, (6)
Таким образом, рассматриваемое решение состоит из трех этапов. Так как алгоритм определения функции является итеративным, то ответ, полученный на данном шаге, возвращается через связь к первому узлу диаграммы для определения результата очередного шага.
Следующие методы вычисления функции имеют аналогичные диаграммы моделей, не требуют иллюстрации и подробного описания, отличаются только формулами вычисления приращения очередного шага.
Рассмотрим решение дифференциального уравнения (1) с помощью усовершенствованного метода Эйлера. Улучшение метода заключается в том, что отрезки, построенные между точками функции, должны быть параллельны касательным, которые проведены к графику функции y’ не на левых краях, а по центру интервалов разбиения. Суммарная погрешность этого метода есть величина О(h2).
Приведем формулу усовершенствованного метода Эйлера для узла «вычисление приращения Dy»:
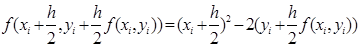 . (7)
. (7)
Приведем формулу усовершенствованного метода Эйлера для узла диаграммы «вычисление функции y»:
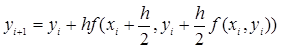 (8)
(8)
Рассмотрим решение дифференциального уравнения (1) с помощью метода Рунге-Кутта четвертого порядка.
Данный метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части f(x, y) уравнения (1). Суммарная погрешность этого метода есть величина О(h4).
Приведем формулу усовершенствованного метода Рунге-Кутта для узла «вычисление приращения Dy»:
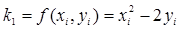 . (9)
. (9)
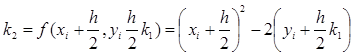 . (10)
. (10)
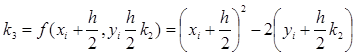 . (11)
. (11)
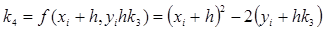 . (12)
. (12)
Приведем формулу усовершенствованного метода Рунге-Кутта для узла диаграммы «вычисление функции y»:
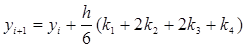 . (13)
. (13)
Сравним полученные результаты расчетов, проведенных в программе «UFOModeler» с точными значениями функции:
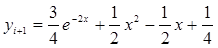 . (14)
. (14)
Вычислим погрешность использованных методов по отношению к точному значению y*. Занесем данные в сводную таблицу.
Таблица
Погрешности вычисления дифференциального уравнения в зависимости от используемого метода
Table
Error of calculation of the differential equation depending on the method used
h шаг | М. Эйлера-Коши | Погреш-ть М. Эйлера-Коши | М. Усов-й Эйлера | Погреш-ть М. Усов-го Эйлера | М. Рунге-Кутта | Погреш-ть М. Рунге-Кутта | Точные значения y* |
0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
0,1 | 0,820500 | 0,001452 | 0,820250 | 0,001202 | 0,819051 | 0,00000283 | 0,819048 |
0,2 | 0,675210 | 0,00247 | 0,674755 | 0,002015 | 0,672745 | 0,00000472 | 0,672740 |
0,3 | 0,559772 | 0,0031632 | 0,559149 | 0,0025401 | 0,556615 | 0,00000569 | 0,556609 |
0,4 | 0,470613 | 0,0036162 | 0,469852 | 0,002855 | 0,467004 | 0,00000650 | 0,466997 |
0,5 | 0,404803 | 0,00389283 | 0,403929 | 0,00301885 | 0,400917 | 0,00000683 | 0,400910 |
0,6 | 0,359938 | 0,00404232 | 0,358972 | 0,00307566 | 0,355903 | 0,00000714 | 0,355896 |
0,7 | 0,334049 | 0,00410142 | 0,333007 | 0,00305876 | 0,329955 | 0,00000727 | 0,329948 |
0,8 | 0,325521 | 0,00409853 | 0,324416 | 0,00299354 | 0,321430 | 0,00000788 | 0,321422 |
0,9 | 0,333027 | 0,00405283 | 0,331871 | 0,00289675 | 0,328982 | 0,00000752 | 0,328974 |
1 | 0,355482 | 0,003981 | 0,354284 | 0,00278301 | 0,351509 | 0,00000764 | 0,351501 |
Исходя из значений, полученных в таблице 1 можно сделать вывод о том, что метод Рунге-Кутта является наиболее близким по отношению к точному значению, погрешность составляет |e| < 0,00001. Метод Эйлера-Коши и усовершенствованный метод Эйлера обладают меньшим классом точности, погрешность данных методов составляет |e| < 0,01.
На основании таблицы построим графики функций. Воспользуемся функцией построения графиков, встроенной в программу «UFOModeler».
На рисунке 2 представлены графики функций, из которых можно сделать вывод о точности приближенных методов решений.
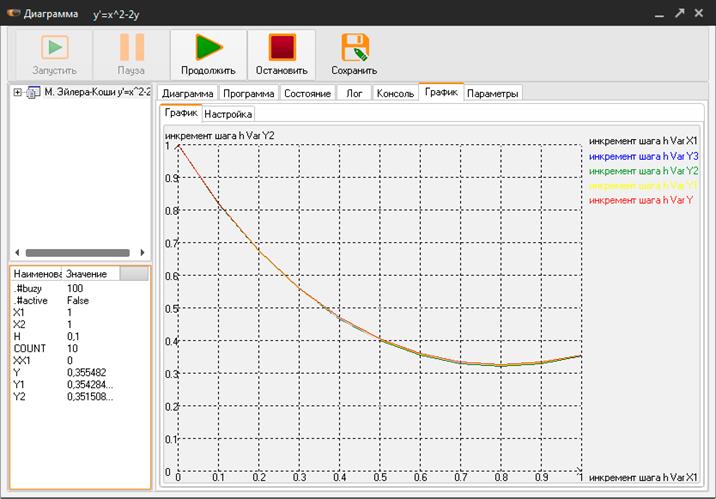
Рис. 2. Различия графиков функций в зависимости от погрешностей
Fig. 2. Differences of graphs of functions depending on the error
Заключение
Таким образом, произведена адаптация УФО-подхода к задаче представления математических данных с целью моделирования процесса решения обыкновенных дифференциальных уравнений.
Разработаны диаграммы, отражающие процесс решения обыкновенных дифференциальных уравнений первого порядка в терминах «Узел-Функция-Объект».
Сформирована сводная таблица результатов вычислений.
Построены графики результирующих функций с помощью программного обеспечения «UFOModeler».
Имитационное программное обеспечение UFOModeler способно вести вычисления с высокой точностью, и может быть использовано для моделирования вычислительных процессов.
















Список литературы
1. Маторин С.И., Попов А.С., Маторин В.С. Моделирование организационных систем в свете нового подхода «Узел-Функция-Объект» // НТИ. Сер. 2. 2005. № 1. С. 1-8.
2. Минский М. Фреймы для представления знаний. М.: Мир. - 1979. - 152 с.
3. Нильсон Н. Принципы искусственного интеллекта. М.: Радио и связь. - 1990. - 376 с.
4. William A. What's in a link: foundations for semantic networks // In: D.G. Bobrow and A. Collins, eds. Representation and Understanding, Academic Press, New York. -1975. pp. 35-82.