СИСТЕМНО-ОБЪЕКТНОЕ ИМИТАЦИОННОЕ МОДЕЛИРВОАНИЕ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ НА ПРИМЕРЕ "МНОГОФУНКЦИОНАЛЬНОГО ЦЕНТРА ПРЕДОСТАВЛЕНИЯ ГОСУДАРСТВЕННЫХ И МУНИЦИПАЛЬНЫХ УСЛУГ"
Aннотация
В данной статье рассматриваться имитационная системно-объектная модель деятельности по оказанию услуг в Государственном автономном учреждении Белгородской области "Многофункциональный центр предоставления государственных и муниципальных услуг".
Рассмотрим применение программного инструментария имитационного моделирования процессов и систем «UFO-modeler» [1] для того, чтобы смоделировать деятельность организации по оказанию услуг и выявить при каком количестве клиентов, очередь будет критичной, а также ответить на вопрос: рационально ли функционирует система массового обслуживания.
В качестве объекта имитационного моделирвоания выступает Государственное автономное учреждение Белгородской области "Многофункциональный центр предоставления государственных и муниципальных услуг" (МФЦ). Для создания модели был произведён сбор данных о количестве обратившихся клиентов, которым были оказаны услуги в конкретном окне и среднее время оказании услуг. Сбор данных был произведен с 01.10.2016 по 31.10.2016. Работа учреждения осуществлялась с понедельника по субботу. Окна, где предоставляются услуги, были сгруппированы по участникам (территориальные органы федеральных органов исполнительной власти, исполнительные органы государственной власти Белгородской области, органы местного самоуправления, городские и районные организации). Количество участников составляет 22, всего доступных окон предоставляющие услуги составляет - 56 из них 44 осуществляли оказание услуг.
Используя исходный набор данных, можно корректно построить модель деятельности учреждения, но для этого требуется произвести вычисления следующих значений: нахождение суммы, среднего значения, диапазона отклонения, процентного распределения заявок и времени оказании услуг, которые сгруппированы по дням недели, значения времени и заявок на один день.
Для нахождения данных относящихся ко времени и заявкам, вычисления выполняются аналогичным образом.
Таблица 1
Фрагмент собранных данных за 1 день
Table 1
Fragment of collected data for 1 day
№ п/п | Участник МФЦ | Номер окна | Количество оказанных услуг | Среднее время ожидания услуги, мин. | Среднее время оказания услуги, мин. |
1 | Отдел приема и выдачи документов МФЦ | Окно 1 | 0 | 0 | 0 |
2 | Управление социальной защиты населения администрации г. Белгорода, МБУ "Центр социальных выплат" | Окно 2 | 24 | 0.23 | янв.32 |
3 | Окно 3 | 39 | 0.40 | фев.40 | |
4 | Департамент строительства и архитектуры администрации г. Белгорода | Окно 4 | 0 | 0 | 0 |
5 | Управление социальной защиты населения администрации г. Белгорода, МБУ "Центр социальных выплат" | Окно 5 | 13 | 0.70 | июл.68 |
6 | УФПС Белгородской области, филиал ФГУП "Почта России" | Окно 6 | 0 | 0 | 0 |
7 |
| Окно 7 | 0 | 0 | 0 |
8 | Комитет строительства администрации Белгородского района | Окно 8 | 0 | 0 | 0 |
9 | ГУП "Белоблтехинвентаризация" | Окно 9 | 6 | июн.43 | дек.77 |
Для нахождения среднего количества заявок или времени оказания услуг из сгруппированных данных, требуется выполнить расчеты по следующей формуле: Sср.=Sобщ./n, где Sср. – среднее количество заявок или время оказания услуги в рассматриваемой группе; Sобщ. – суммарное количество заявок или время оказания услуги по конкретным дням недели; n – количество в рассматриваемой группе.
Диапазон отклонения вычисляется в несколько этапов. Первый этап заключается в нахождении отклонений по каждому дню недели, в каждой группе по следующей формуле: Rx=(Sср - Sx) /100, где x – номер дня недели в конкретной группе; Rx – значение в x день; Sср– среднее количество в рассматриваемой группе; Sx – суммарное значение в x день. Вторым этапом является нахождения по модулю минимального и максимального значения из найденных отклонений в конкретной группе. Полученные два значения и будут являться диапазоном отклонения. Этот диапазон позволит при моделировании получать новое значение, когда наступит новый день.
Следующими вычислениями будут нахождение процентного распределения. Для этого находится среднее значение для каждого окна в каждой группе данных. Среднее значение по каждому окну вычисляется по формуле: Sокно=Sy/n, где Sy – сумма значений по каждому окну; n – количество дней рассматриваемой группе. Затем вычисляется процентное распределение по следующей формуле: Px= (Sокно *100) /Sx), где Px – процентное распределение по конкретному окну; Sокно – среднее значение в конкретном окне; Sx – сумма средних значений по каждому окну за конкретные дни недели; Итоговыми вычислениями является применение процентного распределения и вычисленное значение с отклонением по следующей формуле: Nокно=(( Sср.+ rand)* Px)/100, где rand – случайное число, лежащее в диапазоне отклонения.
Рассмотрим вычисление всех требуемых значений используя группировку данных по понедельникам, найдем сумму всех заявок и поделим на 5, чтобы найти среднее значение заявок по всем понедельникам. Сумма всех заявок за все понедельники - 4276. Среднее количество - Sср =4276/5=855,2.
Найдя среднее количество заявок за понедельники, необходимо вычислить диапазон, который в дальнейшем будет изменять среднее значение заявок по понедельникам. Диапазон отклонения – R1= (855,2-608)/100, R1=2,472. Выполнение подсчета остальных значений производится аналогичным образом, по окончанию подсчета всех значений определяем по модулю максимум и минимум из вычисленных значений. Максимум – 3,518, минимум – 0,368.
Таблица 2
Фрагменты данных, после вычисления среднего количества заявок
Table 2
Fragments of data, after calculating the average number of applications
| Понедельники | |||||||
Окно 2 | 132 | 168 | 285 | 248 | 133 | |||
Окно 3 | 69 | 53 | 291 | 117 | 76 | |||
Окно 5 | 43 | 45 | 183 | 59 | 60 | |||
Окно 6 | 42 | 38 | 72 | 85 | 55 | |||
Окно 7 | 44 | 60 | 40 | 59 | 21 | |||
. . . | ||||||||
Окно 50 | 69 | 32 | 36 | 63 | 55 | |||
Окно 53 | 0 | 0 | 0 | 0 | 0 | |||
Окно 55 | 6 | 4 | 7 | 5 | 8 | |||
Окно 56 | 36 | 41 | 44 | 25 | 43 | |||
Сумма х день | 608 | 661 | 1207 | 892 | 908 | |||
| Сумма всех заявок | 4276 | |||||||
| Среднее количество | 855.2 | |||||||
Следующими вычислениями является нахождение среднего значения по каждому окну за 5 дней – Sокно2=193,2, Sокно3=121,2 и тд.
Таблица 3
Фрагменты данных после вычисления диапазона распределения заявок
Table 3
Data fragments after calculating the range of allocation of applications
| Понедельник | Среднее знач. | ||||
Окно 2 | 132 | 168 | 285 | 248 | 133 | 193.2 |
Окно 3 | 69 | 53 | 291 | 117 | 76 | 121.2 |
Окно 5 | 43 | 45 | 183 | 59 | 60 | 78 |
. . . | ||||||
Окно 53 | 0 | 0 | 0 | 0 | 0 | 0 |
Окно 55 | 6 | 4 | 7 | 5 | 8 | 6 |
Окно 56 | 36 | 41 | 44 | 25 | 43 | 37.8 |
Сумма заявок | 608 | 661 | 1207 | 892 | 908 | 1100.033 |
Сумма всех заявок | 4276 |
|
|
|
| |
Среднее всех заявок | 855.2 |
|
|
|
| |
Диапазоны | 2.472 | 1.942 | -3.52 | -0.37 | -0.53 |
|
Модуль | 2.472 | 1.942 | 3.518 | 0.368 | 0.528 |
|
Мин | 0.368 |
|
|
|
|
|
Макс | 3.518 |
|
|
|
|
|
Следующими действиями будут подсчет процентного распределения «Окно 2» P2=(193,2*100)/1100,033. P2=17,5631. После рассчитывается количество заявок на понедельники с учетом отклонения – 855-2,4=852,6=853. Далее находится количество заявок на 1 день недели – N2=(853*17,5631)/100= 30 заявок. Нахождение для других окон находится аналогично.
Таблица 4
Фрагмент данных при подсчете процентного распределения заявок
Table 4
A fragment of the data in the calculation of the percentage distribution of applications
Процентное распределение по понедельникам | ||||
| % | Кол-во заявок за 5 дней | Кол-во заявок за 1 день | |
Окно 2 | 17.5631 | 149.81328 | 150 | 30 |
Окно 3 | 11.01785 | 93.982243 | 94 | 18.8 |
Окно 5 | 7.090694 | 60.483622 | 60 | 12 |
. . . | ||||
Окно 53 | 0 | 0 | 0 | 0 |
Окно 55 | 0.545438 | 4.6525863 | 5 | 1 |
Окно 56 | 3.43626 | 29.311294 | 29 | 5.8 |
Сумма | 100 | 853 | 853 | 170.7 |
Теперь необходимо произвести вычисления касающихся времени оказания услуг. Сумма времени за все понедельники – 911,8. Среднее количество - Sср =911,8/5=182,4.
Таблица 5
Фрагменты данных, после вычисления среднего количества времени.
Table 5
Fragments of data, after calculating the average amount of time
| Понедельники | ||||
Окно 2 | 2.03 | 1.55 | 2.17 | 1.37 | 1.92 |
Окно 3 | 2.72 | 4.93 | 1.72 | 2.53 | 2.58 |
Окно 5 | 6.83 | 6.72 | 3.3 | 5.77 | 4.48 |
Окно 6 | 8.4 | 26.38 | 6.82 | 4.43 | 13.6 |
Окно 7 | 3.07 | 2.8 | 5.45 | 2.68 | 2.45 |
. . . | |||||
Окно 50 | 6.47 | 9.17 | 7.15 | 5.4 | 6 |
Окно 53 | 0 | 0 | 0 | 0 | 0 |
Окно 55 | 5.48 | 6.78 | 9.03 | 10.45 | 10.1 |
Окно 56 | 5.2 | 4.23 | 4.55 | 5.33 | 4.52 |
Сумма х день | 89.33 | 115.49 | 93.69 | 101.82 | 511.49 |
Сумма всех заявок | 911.82 |
|
| ||
Среднее количество | 182.36 |
|
| ||
Следующими действиями необходимо вычислить диапазон, который в дальнейшем будет изменять среднее значение времени по понедельникам. Диапазон отклонения – R1= (182,4-89,33)/100, R1=0,93034. Выполнение подсчета остальных значений Rx производится аналогичным образом. Так же, как и при вычислении диапазона отклонения заявок, находится и отклонение времени. Максимум – 0,329126, минимум – 0,066874.
Теперь необходимо подсчитать среднее значение суммы времени на каждое окно по всем понедельникам - Sокно2=1,808, Sокно3=2,896 и тд.
Таблица 6
Фрагменты данных после вычисления диапазона распределения времени
Table 6
Data fragments after calculating the time distribution range
| Понедельник | Среднее знач. | ||||||
Окно 2 | 2.03 | 1.55 | 2.17 | 1.37 | 1.92 | 1.808 | |
Окно 3 | 2.72 | 4.93 | 1.72 | 2.53 | 2.58 | 2.896 | |
Окно 5 | 6.83 | 6.72 | 3.3 | 5.77 | 4.48 | 5.42 | |
. . . | |||||||
Окно 53 | 0 | 0 | 0 | 0 | 0 | 0 | |
Окно 55 | 5.48 | 6.78 | 9.03 | 10.45 | 10.1 | 8.368 | |
Окно 56 | 5.2 | 4.23 | 4.55 | 5.33 | 4.52 | 4.766 | |
Сумма времени | 89.33 | 115.5 | 93.69 | 101.8 | 511.5 | 506.1 | |
Сумма всего времени | 911.8 |
|
|
|
| ||
Среднее значение времени | 182.4 |
|
|
|
| ||
Диапазоны | 0.93 | 0.669 | 0.887 | 0.805 | -3.29 |
| |
Модуль | 0.93 | 0.669 | 0.887 | 0.805 | 3.291 |
| |
Мин | 0.067 |
|
|
|
|
| |
Макс | 0.329 |
|
|
|
|
| |
Процентное распределение для «Окно 2» P2=(1,808*100)/506,1. P2=0,357. Далее рассчитывается время на понедельники с учетом отклонения – 182,4+0,09=182,49=183. Далее находится время обслуживания на 1 день недели – N2=(183*0,357)/100=0,653814. Нахождение для других окон находится аналогично.
Таблица 7
Фрагмент данных при подсчете процентного распределения времени
Table 7
Fragment of data in calculating the percentage distribution of time
Процентное распределение по понедельникам | ||
| % | Время обслуживания |
Окно 2 | 0.357 | 0,653814 |
Окно 3 | 0.572 | 1.0415365 |
Окно 5 | 1.071 | 1.9492846 |
Окно 6 | 2.357 | 4.2891453 |
Окно 7 | 0.65 | 1.1832373 |
Окно 8 | 1.212 | 2.2053529 |
. . . | ||
Окно 47 | 1.341 | 2.4402022 |
Окно 48 | 0 | 0 |
Окно 49 | 2.187 | 3.9794896 |
Окно 50 | 1.351 | 2.4592634 |
Окно 53 | 0 | 0 |
Окно 55 | 1.654 | 3.0095227 |
Окно 56 | 0.942 | 1.7140757 |
Сумма | 100 | 183 |
Рассмотрим модель деятельности государственного учреждения в оказании услуг с применением методологии «Узел - Функция-Объект» [2], которая смоделирована и представлена на рисунках 1–4.
На рисунке 1 изображена связь между населением г. Белгорода и государственным учреждением, для моделирования поступления заявок, был создан узел «День недели» имеющий возможность управления днем недели путем использования таймера дня (время работы учреждения). Когда таймер запускается, происходит определение номера дня недели. Затем этот номер передается в следующий узел «Население г. Белгород», позволяющий в зависимости от полученного номера вычислить количество заявок с применением отклонения. Далее это количество вместе с номером дня недели передается в узел «МФЦ» в котором происходит моделирование взаимодействия клиента и учреждения. Подробное описание этого узла представлена ниже. Результатом взаимодействия являются переданные обработанные заявки в узел «Обслуженные клиенты» для их подсчета.
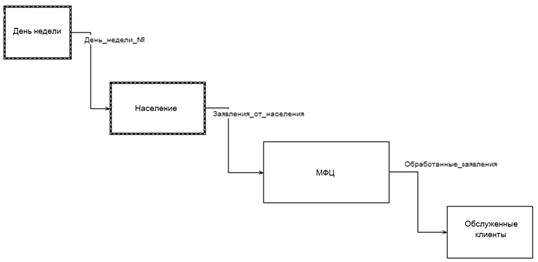
Рис. 1. Контекстная модель
Fig. 1. Context model
Поступающие данные в узел «МФЦ» обрабатываются в узле декомпозиции «Терминал», который моделирует ситуацию, когда клиент берет талон и направляется в нужное окно. Результатом моделирования является увеличение значения заявок в связи между «Терминал» и требуемым окном. Подробное описание декомпозиции узла «Терминал» представлено далее. Каждое окно сгруппировано по узлам (названия узлов соответствуют названиям участников) декомпозиция которых представлена далее. Результатом группы узлов являются значения обработанных заявок, являющиеся в свою очередь входными значениями для суммирования в узле «Выход (обработанные заявления)».

Рис. 2. Фрагмент декомпозиции узла «МФЦ».
Fig. 2. Fragment of the decomposition of the node "MFC"
Декомпозиция узла «Терминал» представляет собой узел «Распределение» получающий номер дня недели, количество заявок. Затем после получения данных, происходит выбор окна путем генерирования случайного числа. Если на исходящей связи узла «Распределение» и входящей связи выбранного узла (окна) стоит специальный флаг, то происходит увеличение количества заявок в этой связи, передача номера дня недели, количество заявок и уменьшение на входящей связи узла «Распределение». Иначе если специальный флаг не стоит, то увеличение заявок не производится и выполняется повторная генерация случайного числа.
Как только были переданные данные выбранному узлу, этот узел выполняет вычисление заявок в соответствии с процентным распределением и с учетом отклонения по конкретному окну. Затем из вычисленного значения вычитаются по мере поступления заявки и передаются далее на обработку. Когда вычисленное значение будет равно 0, специальный флаг снимается и прекращается поступление заявок от узла «Распределение» на этот узел.

Рис. 3. Фрагмент декомпозиции узла «Терминал»
Fig. 3. Fragment of decomposition of the node "Terminal"
Декомпозиция группы узлов отражающих группы участников содержит несколько или один узел, в котором поступившие заявки задерживаются на определенное время. Время задержек зависит от вычисленных ранее значений. Далее заявки передаются в узел сбора заявок «Сумма1», который отправляет для сбора с другими обработанными заявками из других групп.

Рис. 4. Фрагмент декомпозиции узла «Управление социальной защиты населения администрации г. Белгорода, МБУ "Центр социальных выплат»
Fig. 4. Fragment of the decomposition of the node "Administration of Social Protection of Population of the Administration of Belgorod, MBU" Center for Social Payments"
Проведенные эксперименты с применением разработанной модели, показали, что модель является адекватной и позволяет моделировать различные варианты интенсивности поступающих заявок, вычислять среднее время обработки заявок и т.п.
















Список литературы
1. Жихарев А.Г., Маторин С.И., Корчагина К.В. Имитационное моделирование с применением системного подхода и исчисления объектов // Объектные системы – 2016: материалы XII Международной научно-практической конференции (Ростов-на-Дону, 10-12 мая 2016 г.) / Под общ. ред. П.П. Олейника. – Ростов-на-Дону: ШИ (ф) ЮРГПУ (НПИ) им. М.И. Платова, 2016, С. 28-33.
2. S.I. Matorin, A.G. Zhikharev, O.A. Zimovets The elements of general theory of the systems in terms of system-object approach of «Unit-Function-Object» // International Journal of Applied Engineering Research – 2015.- Vol. 10 – No. 24.- P. 44831-44837.