Images, obtained with the help of aerial photographs and artificial satellites, play a significant role in modern cartography. Increasingly, they are used to find the optimal route, analyzing the state of the objects and their identification. Currently, the use of imagery of the earth surface is typical for different spheres of human activities: nature management, agriculture, environmental safety, the land registry, navigation, modeling, cartography, monitoring, energy, etc. Images, obtained with the help of aerial photographs and artificial satellites for analysis added to the database, comparing them with geo-information. Geo-information is the information about geographic location and condition of features, as well as about changes in their condition.

Existing technologies of storage geo-information using database and the corresponding image noticeably increase the traffic to mobile devices when using geo-information. Thus, it seems reasonable to store the image information (geodata) in the image, using secretive coding, without introducing any user-visible distortion and without affecting the system of automatic identification. Methods to carry out covert encoding are called steganography [1, 2].

Fig. 1. The scheme of encoding information

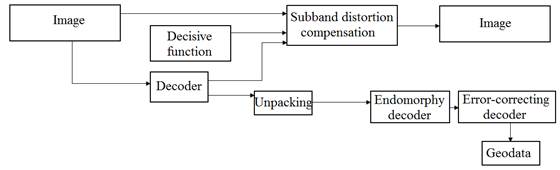
Fig. 2. The scheme of decoding information

Figures 1 and 2 represent a scheme of encoding and decoding geodata in the image.

For concealing information for coding in the image will be used matrix notation, the model is presented below.

Fig. 3. Matrix representation of image: a) image; b) the fragment of image in frequency representation; c) fragment of image size

Figure 3a presents in numerical form, the result of the registration of energy [3] from the visual image of an object or phenomenon, stored, transmitted or used for further reproduction in the form of pixels. The pixel means the smallest indivisible element of the registered image in the spatial domain, which is a quantitative estimate of the energy in the recorded frequency band.

In practice of digital image processing [4-7] there are methods based not on the image itself, but on its discrete cosine transform (DCT). There is a direct discrete cosine transform and an  inverse discrete cosine transform [8-11].

Direct DCT:

                              (1)

where F – a block image size 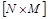, with pixel values ;

 – a block of DCT coefficients size 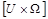, with values ;

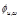D – a DCT matrix, , , .

Inverse DCT:

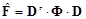,                              (2)

where F – a block of image retrieved from the frequency coefficients of DCT.

The matrix D stores a set of cosine functions in the discrete form, which are necessary to carry out an orthogonal transformation image F (1) and (2) to DCT.

,                                 (3)

where ,  – step selectable frequencies , ; С(l) – coefficients:

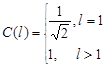,                         (4)

where l corresponds  or .

The method of steganography of Koch-Zhao is based on this mathematical technique. The method consists in encoding bits of information by replacing a valid value of the DCT coefficients selected after preliminary analysis of the frequency domain of the image. The preliminary analysis allowing selecting frequency coordinates is known before a decisive rule. Encoding and decoding are performed in the DCT coefficients.

Figure 4 represents a known frequency image model, which carried out the separation of the matrix of coefficients of DCT on the frequency domain. Thus, the lowest frequency is located in the upper left corner of the image, and the highest – in the lower right. It is known that the most effective is the encoding of information in the field of mid frequencies, because low frequencies contain the most part of the energy of the image, and high frequencies – are most susceptible to the distortion of a communications channel and more easily influenced during processing.

Evaluation of the distortions introduced in the image after secretive encoding are determined by the correlation equation (5) that evaluates the similarity measure between the initial image fragment and the fragment with the covertly encoded information.

                          (5)

where 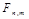 – a pixel of the original image fragment ;

 – a pixel with the covertly encoded information in the image fragment ;

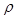 – the degree of correlation between the image  and the image .

Fig. 4. Frequency model of image

The results of calculations are presented in table 1. The main drawback of the method and, in general, the methods used to encode the frequency region, is the use of DCT for all pixels of the image that does not allow spatial selectivity. As can be seen in figure 5, when changing the coefficients located in the low frequency region, and with increasing frequency encoding (Fig. 5 b-d) in the image there appears a significant distortion, such as blemishes and ripples. Since the ratio (1; 1) contains information about the constant component of the signal, as it changes the image into a completely shaded one (Fig. 5b). This feature is connected with the energy distribution in the image.

а)                                    b)                                    c)

d)                                                e)

In the process of the preliminary research, it was noted that the information encoded in the high frequency and mid-frequency regions is less resistant to external influences compared with information encoded in the low frequency region. However, as can be seen in table 1 and the previously shown Fig. 5 b-d, distortion in the high frequency and mid-frequency regions is significant. Therefore, it is necessary to develop a more selective method of encoding covert, in which all transformations and analysis will occur in a spatial region with minimal losses.Fig. 5. The fragment of image: a) input; b) by inverting the DCT coefficients with coordinates (1,1); c) by inverting the DCT coefficients with coordinates (3,1); d) by inverting the DCT coefficients with coordinates (6,7); e) by inverting the DCT coefficients with coordinates (45,46)

The mathematical basis of the proposed method is a subband transformation [3, 4].

The direct subband transformation is performed by using a receiving subband projection (6), wherein the core of the subband matrix has a form (7). The reverse transformation takes place by a line-by-line scalar product of the transpose of the matrix of eigenvectors for the matrix of subband projection (8).

Table 1

Evaluation of the distortion caused by embedding the information using the Koch–Zhao method

Frequency domain	№ of experiment	Coefficients		Correlation,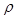
1	2	3	4	5
LF	1	1	2	0.9864
		2	1
LF	2	1	1	∞
		2	2
LF	3	1	3	0.8072
		3	1
LF	4	5	6	0.9699
		6	5
LF	5	6	5	0.9865
		7	8
LF	7	9	10	0.9978
		10	9
MF	6	25	12	0.9981
		26	13
MF	8	10	30	0.9998
		30	10
MF	9	37	38	0.9999
		38	37
HF	10	45	46	Close to 1
		46	45
HF	11	62	63	Close to 1
		63	62

The direct subband transformation (generate subband projection):

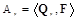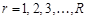,                        (6)

where F – a block of image size 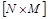 with the pixel values ;

A_r – a the vector-matrix containing the values of subband projections;

Q_r – the matrix, the rows of which are eigenvectors of the subband matrix [4, 5].

The core of the subband matrix has a form:

                     (7)

where  ,  – the step of the discrete frequencies , .

L_rQ_r=B_rQ_r,

where L_r – the matrix of eigenvalues.

Reverse subband transformation:

,                (8)

where F – a block of image restored from the values of subband projections.

( ) – the transpose operation;                            

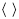 – the row-wise dot product.

Figure 6 proposes a model image in subband domain, given for one line of the image. To reduce the seepage in the adjacent frequency domain eigenvalues of the subband matrix it is advisable to pick them up in such a way that they would be close to one. Therefore, for the image shown earlier, and the implementation of the encoding in a single string, the frequency band was divided into R=12 frequency intervals, with the first two numbers were close to one, respectively, the coding was carried out in the corresponding projections.

The subband method of secretive coding of an image is performed in the spatial domain of the image without transition frequency in (9), but the number of decision rules allows to choose the frequency band for encoding, the degree of infiltration in an adjacent lane, the amount of introduced distortion, as well as to determine the stability of geodata to distortions (e.g., noise).

Fig. 6. Model of image in frequency domain

Decoding is the same in the spatial domain.

It is worth noting that the proposed method of subband coding allows recovering the original pixel values, knowing only decision rules that have been coded. The difference in energy between the restored and original image, according to the experiment is 10^-16.

The encoding algorithm:

1.     The image represented in a digital form that is split into blocks  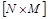pixels.
2.     To represent the geodata in the form of symbols .
3.     To choose the number of frequency regions R.
4.     To calculate the subband matrix L_rQ_r=B_rQ_r.
5.     To find decomposition of the subband matrix B_r on the eigenvectors 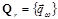 and eigenvalues L_r, , .
6.     To find the projection of the line: , , , .
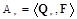7.     According to several decision rules, to choose subband projection: .
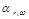8.     According to the encoded symbol  to encode:

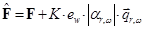.                      (9)

The decoding algorithm:

1.     The image represented in a digital form that is split into blocks   pixels.
2.     To represent the geodata in the form of symbols .
3.     To choose the number of frequency regions R (must be matched with the encoder).
4.     To calculate the subband matrix L_rQ_r=B_rQ_r.
5.     To find decomposition of the subband matrix B_r on the eigenvectors  and eigenvalues L_r, , .
6.     To find the projection of the line: , , , .
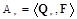7.     According to several decision rules, to choose subband projection: .
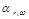8.     To carry out decoding, .

The proposed algorithm allows carrying out the adaptive subband encoding in the specified frequency-spatial domain. It should be noted that for coding information there must be used one-dimensional decomposition. Secretive coding was carried out for all lines, therefore, the throughput of the method above is not less than 64 times more effective in comparison with the method of Koch-Zhao.

Figure 7 and table 2 show the results of a computational experiment for steganographic encoding of information in the image using subband projections. One can see that the distortion is manifested in the form of "ripples" (spatial harmonic signal). The distortion in the form of the ripples is less visible on the fragments having the same intensity, in the case of change of the intensity the ripples increase (figure 7 c, d), and correlation decreases. To minimize these distortions it is necessary to develop additional decision rules, which can realize the selectivity in the spatial domain.

а)                                    b)                                    c)

d)                                                e)

Fig. 7. The fragment of image: a) input; b) by inverting the subband coefficients with coordinates (1,1) – low frequency domain; c) by inverting the subband coefficients with coordinates (10,1) – high frequency domain; d) by inverting the subband coefficients with coordinates (2,1) – low frequency domain; e) by inverting the subband coefficients with coordinates (4,1) – mid-frequency domain

Table 2 presents the results of the experiment for the method of subband projections. By encoding the same portion of an image, distortion in all frequency regions becomes much fewer and, consequently, the correlation increases.

Table 2

Evaluation of the distortion caused by embedding the information using the method of subband projections

Frequency domain	№ of experiment	Coefficients		Correlation,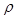
		r	j
1	2	3	4	5
LF	1	1	1	0.9164
LF	2	1	2	0.9999
MF	3	4	1	0.9989
MF	4	4	5	0.9987
MF	5	4	10	Close to 1
MF	7	4	30	0.9999
MF	6	6	15	Close to 1
MF	8	6	30	Close to 1
MF	9	6	50	0.9999
HF	10	11	50	Close to 1
HF	11	12	60	Close to 1

The advantage of the proposed method compared to the existing method is in the increased bandwidth when using fragments greater than 64 pixels, the smaller degree of distortion, the possibility of selectivity in the spatial and frequency domain, inherent in the mathematical model. This is achieved through a mathematical apparatus and the proposed method of encoding.Thus, the proposed steganographic method in digital image processing allows for encoding geodata directly in the image without noticeable deterioration of visual quality.

Работа выполнена при поддержке гранта РФФИ 15-07-01570 (Субполосная скрытная интеграция/извлечение дополнительной информации в аудио или видео контентах) / The work is executed with the support of RFBR grant 15-07-01570 (Subband secretive integration/extraction of additional information in audio or video content).