DEVELOPMENT OF METHODS FOR SOLVING THE TASKS OF THE CONTINIUM LINEAR PROGRAMMING USING LEGENDRE POLYNOMIALS
Abstract
The article demonstrates the theoretical foundations of the mathematical apparatus − the continuum of linear programming. It demonstrates a technique for solving problems with the use of orthogonal systems of functions. The article was an exact solution of the problem of variational calculus to linear constraints. The purpose of the work is to develop accurate methods of solving the problem in the class of Legendre polynomials. The study demonstrates an ability to build the exact solution of the problem and the conditions under which the decision is allowed. Based on the properties of Legendre polynomials, an exact solution of the problem of continual linear programming is provided, in which the integrands and functional limitations are presented in rows of finite degree. Analytically, it is proven that the solution obtained is a limiting case of the linear combination of delta functions. It is shown that the parameters of the optimization problem of finding the unknown functions plan contains half of the variables than in the canonical method. Recommendations are given for the construction of the optimization algorithm. There is a possibility of extending the proposed technology solution in the direction of using other systems of orthogonal polynomials.INTRODUCTION
The simplest of these tasks can be solved by conventional means, if it is the class of functions in which a decision is based [1, p.25]. It was found that the quality of the solution is higher the more "a delta" has a character of its analytical solution. It is shown that the exact solution of the simplest problem of continual linear programming must be sought in the class of delta functions [1, p.48]. In general, the synthesis problem can be formulated as follows: Let the input of a linear system with a known frequency response signal is, the spectral power is described by the function. Find a function that maximizes functional:
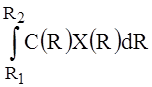 ,
, 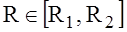 (1)
(1)
and satisfying the limits for the spectral power of the signal system.
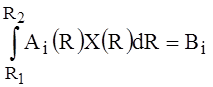 ,
, 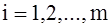 (2)
(2)
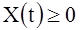 , (3)
, (3)
where C(R), Ai(R) - are integrated in the R function. The research in this article is dedicated to the development of exact methods for solving the above problem of continual linear programming (1)-(4).
1. THE FORMULATION OF THE PROBLEM IN THE CLASS OFLEGENDRE POLYNOMIAS
Let’s introduce the variable t [1, p.24]:
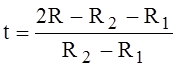 ,
, 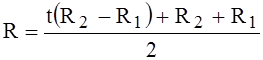 (4)
(4)
with provision of which, we will get the next presentation of our problem:
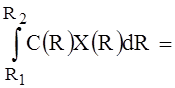
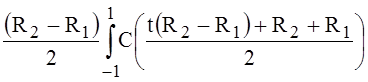
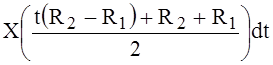 , (5)
, (5)
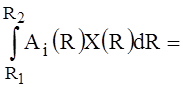
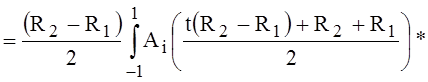
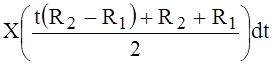 , (6)
, (6)
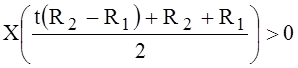 . (7)
. (7)
Using the labeling for c(t) ai(t), x(t):
 ,
,
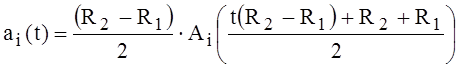 , (8)
, (8)
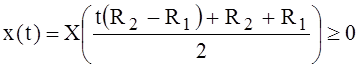 . (9)
. (9)
Let’s present the problem in a canonical form:
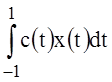 (10)
(10)
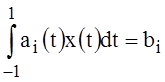 ,
, 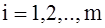 , (11)
, (11)
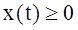 , (12)
, (12)
where c(t), a(t) because of integrability of C(R), Ai(R) on the interval are the integrable functions on the interval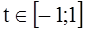 .
.
If the limits of the integration in (1) and (2) are respectively different and equal R21,R11 for (1) and R21,R12 (2) then selecting, 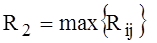 ,
, 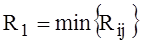 , (i=1,2; j=1,2) and setting function C(R)=0 for
, (i=1,2; j=1,2) and setting function C(R)=0 for 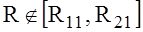 , Ai(R)=0 for
, Ai(R)=0 for 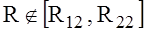 , when the problem is reduced to the form (1)-(3).
, when the problem is reduced to the form (1)-(3).
2. SOLUTION OF THE PROBLEM IN THE CLASS OF LEGENDRE POLYNOMIALS
The solution x(t) is presented on the interval 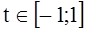 in the form of an expansion in Legendre polynomials P(t) [4, p.64–74]:
in the form of an expansion in Legendre polynomials P(t) [4, p.64–74]:
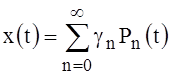 ,
, 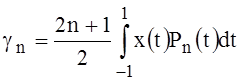 ,
, 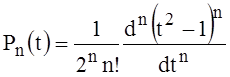 . (13).
. (13).
Representing the specified functions c(t), ai(t) (8) in the form of a convergent series, i=1,2,...,m:
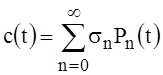 ,
, 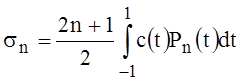 , (14)
, (14)
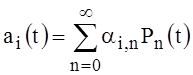 ,
, 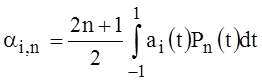 , (15)
, (15)
let’s comply the integration (10), (11) of the formula [4, p.71]:
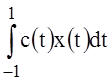 =
=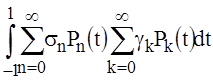
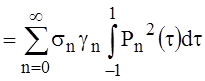 =
=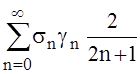 , (16)
, (16)
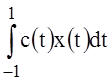 =
=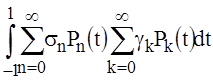
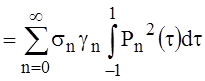 =
=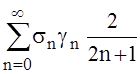 , (17)
, (17)
and we’ll get the statement of the problem, which consists in maximizing function
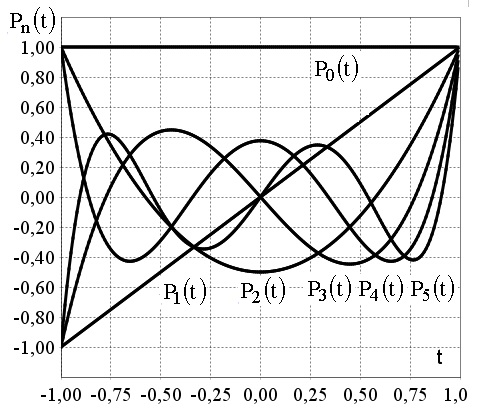
Fig. 1. Legendre’s polynomials Pn(t), n=0,1,2,3,4,5
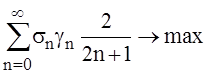 , (18)
, (18)
satisfying constraints
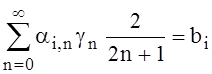 , i=1,2,...,m, (19)
, i=1,2,...,m, (19)
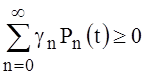 ,
, 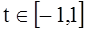 . (20)
. (20)
Let’s deal with the solution of the problem (10)-(12) for the case when the functions C(R), Ai(R) are represented by polynomials of degree N1, N2:
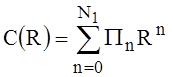 ,
, 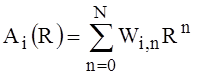 , (21)
, (21)
with coefficients 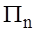 and Wi,n. These include the problem of the LPC, which limits (2) defines the moment of order
and Wi,n. These include the problem of the LPC, which limits (2) defines the moment of order 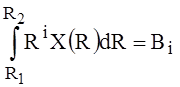 to the range of variation of a random variable
to the range of variation of a random variable 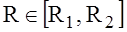 , [1, p.13-17]. The expression tN can be represented by the expansion of the form [5,p.79]:
, [1, p.13-17]. The expression tN can be represented by the expansion of the form [5,p.79]:
tN=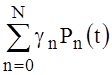 ,
, 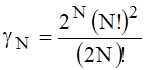 ,
, 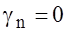 , (22)
, (22)
when (N-n) is odd number,
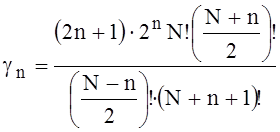 , (23)
, (23)
when (N-n) is even integer, which contains the finite number N Legendre’s polynomials Pn(t).
3. THE USAGE OF LEGENDRE POLYNOMIALS FOR CONSTRUCTING EXACT SOLUTIONS
Let’s imagine, that C(R) and Ai(R) are polynomials R degree N1 and N2, N1>N2. In the view of the identities (22), (23) with (8) functions c(t), ai(t) are polynomials and the degree N1 and N2 with the expansion coefficients 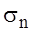 ,
, 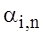 , respectively (14) and (15). We represent the right side of (11) integral with the integrand containing Legendre polynomials,
, respectively (14) and (15). We represent the right side of (11) integral with the integrand containing Legendre polynomials,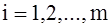 :
:
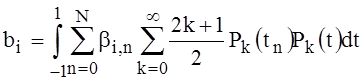 , (24)
, (24)
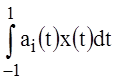 =
=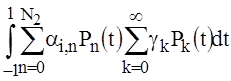
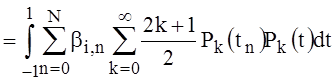 , (25)
, (25)
and we will get an equation that must be solved for 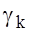 ,
, 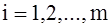 :
:
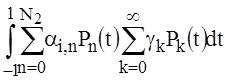
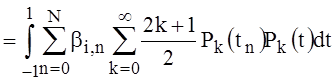 . (26)
. (26)
In the view of orthogonal polynomials Pk(t) expression (26) can be presented as:
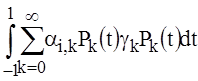 =
=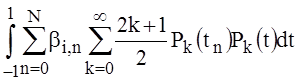 ,
, 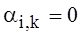 , (27)
, (27)
when k>N2. The solving for 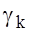 we will present as next
we will present as next
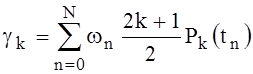 . (28)
. (28)
By substituting (28) into (27) we obtain
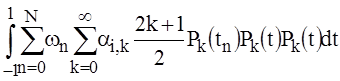
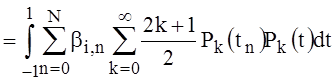 . (29)
. (29)
The solving is next:
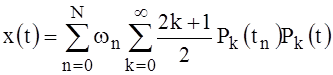 , (30)
, (30)
where 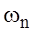 the constants of integration. The right side of formula (30) can be written as follows:
the constants of integration. The right side of formula (30) can be written as follows:
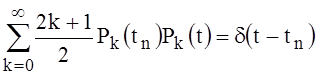 , (31)
, (31)
that allows to present the solution (30) this way:
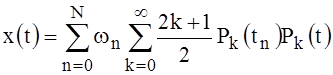 =
=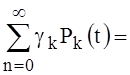
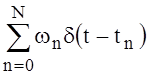 (32)
(32)
Indeed, integrating with the left side of (29), taking into account (15) we obtain:
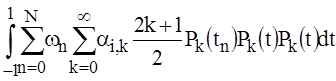
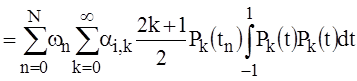
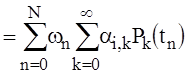 =
= 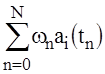 . (33)
. (33)
On the other hand, using (32), a similar result can be written:
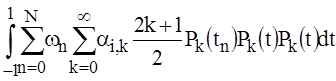 =
=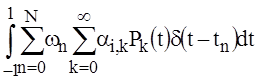 =
=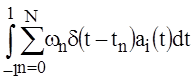 =
=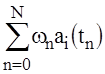 . (34)
. (34)
An important fact is that if the coefficients 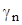 of one and quite simply determined by (11), (25),
of one and quite simply determined by (11), (25), 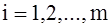 :
:
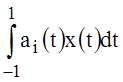 =
=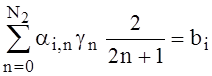 . (35)
. (35)
The rest (N1-N2) of the coefficients 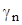 are determined from (18) with the unambiguous representation (28), (31). It should be noted that by virtue of (28) to determine
are determined from (18) with the unambiguous representation (28), (31). It should be noted that by virtue of (28) to determine 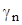 the condition
the condition 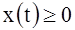 will be satisfied when
will be satisfied when 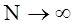 . This condition limits the range of acceptable solutions (10)-(12).
. This condition limits the range of acceptable solutions (10)-(12).
4. AN ALGORITHM FOR SOLVING THE SIMPLEST PROBLEM
Consider the exact solution of the problem (1)-(3) for functions C(R)=1-R2, A0(R)=1 [1, p.24]:
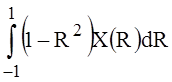 ,
,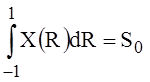 ,
, 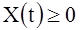 ,
,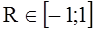 . (36)
. (36)
Using (8) and (9) represent the task (36) in the form:
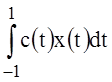 ,
, 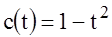 , (37)
, (37)
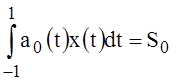 ,
, 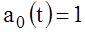 , (38)
, (38)
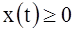 ,
,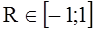 (39)
(39)
Functions c(t) (37), a0(t) (38) in a series in Legendre polynomials
c(t)=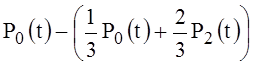 =
=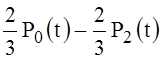 , a0(t)=P0(t), (40)
, a0(t)=P0(t), (40)
where 1=P0(t), 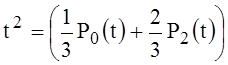 . This allows you to write the problem (37)-(39) as (18)-(20) as follows:
. This allows you to write the problem (37)-(39) as (18)-(20) as follows:
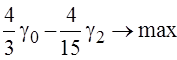 , (41)
, (41)
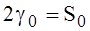
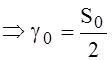 , (42)
, (42)
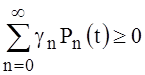 ,
,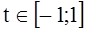 . (43)
. (43)
Since (42) a0(t) is represented by one member of the decomposition a0(t)=P0(t) (40), the search 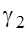 for maximizing the functional (37) use the equation (32), N=1, equating the coefficients in different k:
for maximizing the functional (37) use the equation (32), N=1, equating the coefficients in different k:
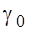 =
=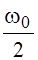 , k=0,
, k=0, 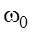 =
=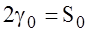 , (44)
, (44)
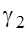 =
=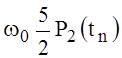 , k=2. (45)
, k=2. (45)
Substituting 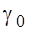 (42),
(42), 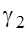 (43) to (41), we define tn in which the expression (41) takes the maximum value:
(43) to (41), we define tn in which the expression (41) takes the maximum value:
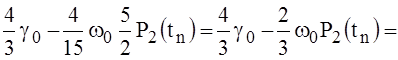
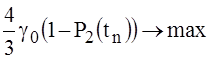 (46)
(46)
The function has a maximum value of the functional (37) is reached at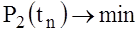 . Where should be
. Where should be 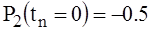 . Thus:
. Thus:
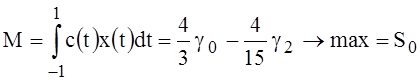 , (47)
, (47)
when
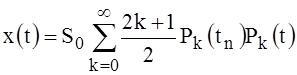 . (48)
. (48)
Figure 2 shows the behavior of the functional value of M (47) depending on the number of polynomials in the solution x(t) (48) for S0=1. It can be seen that when k>2 no functional change its value remains constant. This result is due to the finite number of polynomials Pn(t) in the expansion of c(t) (40).
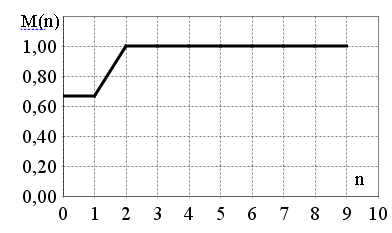
Fig. 2. The dependence of the value of the functional M(n) (46) on the number n of the Legendre polynomials Pn(t) in the solution x(t) (47) for the case S0=1
The solution (37)-(39) is shown in Figure 3. It can be seen that an increase in terms of expansion solution presented in the form of (32) takes a delta character. Each of the solutions presented provides a value of the functional (10) M=1 if the constraint for S0=1 (11). However, compliance with the inequality 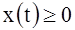 is satisfied for
is satisfied for 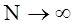 .
.
Fig. 3. Accuracy representation x(t) (47) for the case S0=1 according to the n in the expansion of Legendre polynomials Pn(t)
CONCLUSION
Investigation of properties of solutions of the continuum of linear programming have led to the following conclusions, which are as follows:
1. If the functions c(t) and ai(t) are represented by finite power series of the form (21), the problem (10)-(12) has an exact solution 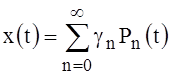 presented Legendre polynomials (13).
presented Legendre polynomials (13).
2. For calculating the coefficients 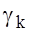 determining the form of the solution x(t), we get easy and convenient for practical calculation formula (28).
determining the form of the solution x(t), we get easy and convenient for practical calculation formula (28).
3. Analitically shown that the solution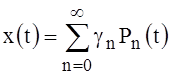 degenerates into a superposition of delta functions, which confirms the conclusions drawn in [1, p.126] - the solution (10) - (12) must be sought as a linear combination of delta functions.
degenerates into a superposition of delta functions, which confirms the conclusions drawn in [1, p.126] - the solution (10) - (12) must be sought as a linear combination of delta functions.
4. Usage of the orthogonal system of functions allowed to formulate noniteration ability to exact solution (30) of the problem (10)-(12).
5. If for c(t) (14) and ai(t) (15) do not permit expansion in an orthogonal set of functions in a finite series, then the solution may be found with a given accuracy. Its value is determined by the accuracy of representation of the specified functions c(t) and ai(t) finite power series (14), (15).
















Reference lists