Введение

При анализе систем автоматического управления c распределенными параметрами одной из важнейших задач является анализ переходных процессов [6, 9, 10]. В системах управления с распределенными параметрами эта задача с математической точки зрения сводится к поиску общего решения некоторого интегро-дифференциального уравнения при заданных начальных и граничных условиях, а также при заданных воздействиях [6, 7]. В большинстве случаев для распределенных систем управления не всегда возможно получить решение в явном виде или установить явную зависимость между параметрами системы и видом решения. Поэтому в теории автоматического управления широко используются приближенные методы анализа переходных процессов [4]. В частности, применение частотных методов позволяет без нахождения собственных значений и собственных функций дифференциальных уравнений осуществлять анализ переходных процессов сосредоточенных систем высокого порядка и систем с распределенными параметрами. Частотный метод анализа переходных процессов основан на использовании частотных характеристик, которые могут быть определены по передаточной функции системы или из эксперимента. При этом передаточная функция системы может быть не только дробно-рациональной, но и трансцендентной функцией [2]. Поэтому данный метод является универсальным и позволяет решать задачу построения переходных процессов систем управления, содержащих как сосредоточенные, так и распределенные параметры.

1. Частотный метод расчета переходных характеристик

Пусть , , — некоторая передаточная функция исследуемой системы управления. Будем предполагать, что  — аналитическая функция в правой полуплоскости и на мнимой оси комплексной плоскости . Пусть, кроме того, g(t) — произвольное задающее воздействие системы, для которого существует изображение по Лапласу. Тогда изображение по Лапласу для переходного процесса определяется формулой

.                                                           (1)

Как известно [3], формула (1) в пространстве оригиналов представляет собой свертку

, .                                                          (2)

Здесь  — импульсная характеристика системы с передаточной функцией , т.е. реакция системы с передаточной функцией  на входной сигнал в виде дельта-функции Дирака при нулевых начальных условиях.

Таким образом, задача построения переходных процессов в системе управления при произвольном входном воздействии сводится к интегрированию некоторого выражения, содержащего импульсную характеристику рассматриваемой системы.

Выражение для переходного процесса x(t) имеет вид [3]

,    ,                                                      (3)

где

,                                                                         (4)

 — абсцисса абсолютной сходимости функции ; в полуплоскости  изображение  — аналитическая функция. Из формулы (3) после элементарных преобразований получаем следующее выражение для переходного процесса [5]:

,         .                                                      (5)

Если , то формула (5) приобретает вид

,       .                                                          (6)

Так как  при t<0, то из (6) получаем

.                                                                    (7)

Пусть , где  и  — соответственно вещественная и мнимая частотные характеристики. При этом,  — четная, а  — нечетная функции аргумента . Тогда, складывая формулы (6) и (7), получаем следующее выражение:

                                                   (8)

Вычитая из выражения (6) выражение (7), имеем

                                                (9)

2. Построение импульсной характеристики и переходного процесса

Для нахождения импульсной характеристики положим , где  — дельта-функции Дирака. Так как изображение по Лапласу для дельта-функции Дирака определяется формулой

,                                                                               (10)

то формула (1) принимает вид

.                                                                           (11)

Так как  — передаточная функция устойчивой системы управления, то  является аналитической функцией в правой полуплоскости комплексной плоскости и на мнимой оси и поэтому можно положить . Тогда импульсная характеристика  может быть найдена по формулам (8) или (9), т. е.

,                              (12)

где  и  — соответственно вещественная и мнимая частотные характеристики .

Для построения переходного процесса при произвольном входном воздействии воспользуемся формулой свертки (2). Так как импульсная характеристика может быть вычислена по формулам (12) и входное воздействие g(t)  известно, то применяя описанные выше формулы для численного интегрирования несобственных интегралов, можно найти реакцию распределенной системы управления на произвольное входное воздействие g(t) .

Следует отметить, что при исследовании систем управления наряду с импульсной характеристикой рассчитываю переходную характеристику h(t) , т.е. реакцию системы на входной сигнал в виде функции Хевисайда (функции единичного скачка) при нулевых начальных условиях. Согласно определению переходной характеристики положим g(t)=l(t) , где l(t)  — функция Хевисайда. Тогда переходная характеристика системы h(t) в силу формулы (2) и определения функции Хевисайда имеет вид

, .                                                 (13)

Для непосредственного вычисления импульсной характеристики в соответствии с формулами (12) следует использовать методы численного интегрирования несобственных интегралов. В частности, можно использовать следующий подход [1]. Для вычисления интеграла вида

                                                           (14)

представим J как сумму определенно интеграла J₁ по конечному промежутку [a, b]  и несобственного интеграла J₂  по промежутку , т. е.

.                                 (15)

Здесь  — некоторое число, которое следует выбирать из условия

                                                                (16)

для произвольного наперед заданного числа . При этом можно использовать прием, который заключается в автоматическом изменении b, например, как b₀ , 2b₀ , 4b₀ , 8b₀ и т. д., где b₀  — начальное значение b, с контролем на каждой i-й стадии условия

.                                                             (17)

Интеграл J₁  можно вычислять с помощью метода Гаусса. Метод Гаусса основан на интерполяции f(z) полиномом Лагранжа, но абсциссы z_i  выбираются из условия обеспечения минимума погрешности интерполяции. При этом интеграл J₁ подстановкой

                                                                 (18)

сводится к виду

.                                                          (19)

Метод Гаусса обеспечивает повышенную точность — формула верна для полиномов до -й степени. Для  имеем

.                                                             (20)

Остаточный член (погрешность) при этом равен

                                                            (21)

Для повышения точности интегрирования отрезок [a, b] дробится на m частей.

3. Примеры

С помощью описанной выше методики построим переходную характеристику для системы управления с передаточной функцией

.                                                                          (22)

Нетрудно проверить, что переходная характеристика для данной системы имеет вид

.                                                                            (23)

На рис. 1 представлены точная и расчетная переходные характеристики для системы управления с передаточной функцией (22). Очевидно, что кривые совпали.

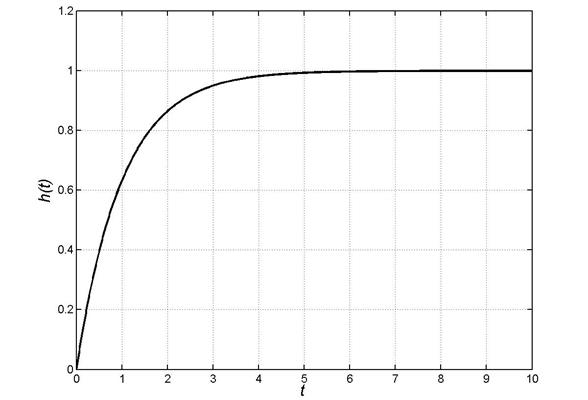
Рис. 1. Переходные характеристики

Fig. 1. Transient responses

На рис. 2 представлена переходная характеристика для распределенной системы управления со следующей передаточной функцией [8]:

.                                                                    (24)

Все расчеты и графические построения были проведены в пакете Matlab.

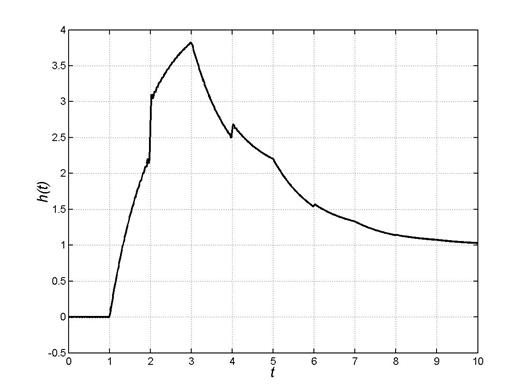
Рис. 2. Переходная характеристика

Fig. 2. Transient response

Работа выполнена в соответствии с Госзаданием № 1.759.2016/ДААД “Проведение научно-исследовательских работ в рамках международного научно-образовательного сотрудничества по программе «Михаил Ломоносов» по теме: «Моделирование и регулирование линейных систем с распределёнными параметрами»”.